
����Ŀ���ۺ��⡣
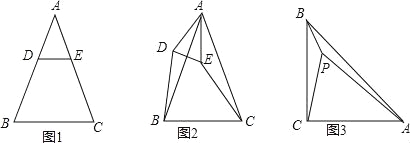
��1����ͼ�٣���ABC�У���D��E�ڱ�BC�ϣ�AEƽ�֡�BAC��AD��BC����C=40�㣬��B=60�㣬�١�CAE�Ķ������ڡ�DAE�Ķ�����
��2����ͼ�ڣ����ѣ�1���е�������AD��BC����ɡ�FΪAE�ӳ�����һ�㣬��FD��BC���������������䣬�����DFE�Ķ�����
��3���ڡ�ABC�У�AEƽ�֡�BAC����FΪEA�ӳ�����һ�㣬FD��BC���ҡ�C=������B=�£��£��������Բ����DFE�Ķ������æ����±�ʾ�������Լ�������Ӧͼ�β�˵�����ɣ� 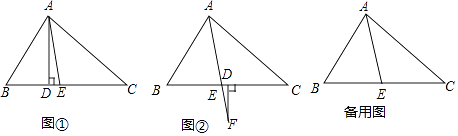
���𰸡�
��1���⣺��ͼ��1����
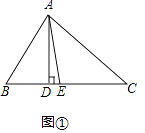
��AD��BC��
���ADB=90�㣬
���BAD=90�㩁��B=90�㩁60��=30�㣬
�ߡ�BAC=180�㩁��B����C=180�㩁60�㩁40��=80�㣬
��AEƽ�֡�BAC��
���BAE= ![]() ��BAC=
��BAC= ![]() ��80��=40�㣬
��80��=40�㣬
���DAE=��BAE����BAD=40�㩁30��=10�㣻
��2���⣺��ͼ2�У���AH��BC��H��
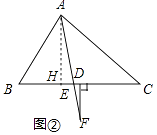
�ɣ�1����֪��HAE=10�㣬
��AH��EF��
���DFE=��HAE=10��
��3���⣺���ۣ���DFE= ![]() ����B����C�����������£�
����B����C�����������£�
��ͼ3�У���AH��BC��H��FD��BC��D��
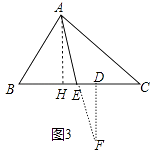
�ߡ�HAE=��EAB����BAH����BAH=90�㩁��B����BAE= ![]() ��180�㩁��B����C����
��180�㩁��B����C����
���HAE=90�㩁 ![]() ��B��
��B�� ![]() ��C����90�㩁��B��
��C����90�㩁��B��
= ![]() ����B����C����
����B����C����
��AH��FD��
���DFE=��HAE��
���DFE= ![]() ����B����C����
����B����C����
����������1����ͼ1�У������BAD����BAE�����ݡ�DAE=��BAE����BAD���ɽ�����⣮��2����ͼ2�У���AH��BC��H�����ã�1���н��ۣ���֤����DFE=��HAE���ɣ���3�����ۣ���DFE= ![]() ����B����C������ͼ3�У���AH��BC��H��FD��BC��D���ɡ�HAE=��EAB����BAH����BAH=90�㩁��B����BAE=
����B����C������ͼ3�У���AH��BC��H��FD��BC��D���ɡ�HAE=��EAB����BAH����BAH=90�㩁��B����BAE= ![]() ��180�㩁��B����C���Ƴ���HAE=90�㩁
��180�㩁��B����C���Ƴ���HAE=90�㩁 ![]() ��B��
��B�� ![]() ��C����90�㩁��B��=
��C����90�㩁��B��= ![]() ����B����C������AH��FD���Ƴ���DFE=��HAE�����ɽ�����⣮
����B����C������AH��FD���Ƴ���DFE=��HAE�����ɽ�����⣮
�����㾫����������Ŀ����֪���������������ε��ڽǺ���Ǻ������ε���ǵ����֪ʶ���Եõ�����Ĵ𰸣���Ҫ���������ε������ڽ��У�ֻ������һ���ڽ���ֱ�ǻ�۽ǣ�ֱ�������ε�������ǻ��ࣻ�����ε�һ����ǵ��ں��������ڵ������ڽǵĺͣ������ε�һ����Ǵ����κ�һ�����������ڵ��ڽǣ�������һ������һ�ߵ��ӳ�����ɵĽǣ��������ε���ǣ������ε�һ����ǵ��ں��������ڵ������ڽǵĺͣ������ε�һ����Ǵ����κ�һ�����������ڵ��ڽǣ�


 �¿α�������������ҵ�������γ�����ϵ�д�
�¿α�������������ҵ�������γ�����ϵ�д� ����ν����Ž̲��㽭���̴�ѧ������ϵ�д�
����ν����Ž̲��㽭���̴�ѧ������ϵ�д� �����Ļ������������������ϵ�д�
�����Ļ������������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
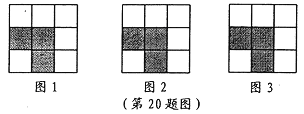
����Ŀ��������8�֣�����3��3��������9����ͬС��������ɣ�ÿ������ͼ����3��С��������Ϳ����Ӱ���������µ�6���հ�С�������У�������Ҫ��Ϳ����Ӱ��
��1��ѡȡ1��Ϳ����Ӱ��ʹ4����ӰС���������һ����Գ�ͼ�Σ����������ĶԳ�ͼ�Σ�
��2��ѡȡ1��Ϳ����Ӱ��ʹ4����ӰС���������һ�����ĶԳ�ͼ�Σ���������Գ�ͼ�Σ�
��3��ѡȡ2��Ϳ����Ӱ��ʹ5����ӰС���������һ����Գ�ͼ�Ρ�
���뽫����С������������ͼ1��ͼ2��ͼ3�У���ֻ�軭������������һ�����Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����ȷ���ǣ� ��
A.�Ȼ����Ե�Բ�Ľ����B.�Ż�һ�������ӻ�
C.�������������һ��ԲD.��ȵ�Բ�Ľ����ԵĻ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������У�����������ͬʱʹ�ã��ܽ������̵��ǣ� ��
A.��ʮ������
B.��ʮ����
C.���˱���
D.�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABC�ǵ��������Σ�AB=AC��
��1���������Σ���ͼ1����DE��BCʱ����DB EC�������������������=����
��2������̽��������ͼ1�е���ADE�Ƶ�A˳ʱ����ת����0�㣼����180�㣩��ͼ2λ�ã���1���еĽ��ۻ��������������������֤����������������˵�����ɣ�
��3����չ���ã���ͼ3��P�ǵ���ֱ��������ABC��һ�㣬��ACB=90�㣬��PB=1��PC=2��PA=3������BPC�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڳ�����ABCD�У��ѡ�BCD�ضԽ���BD�۵��õ���BED���߶�BE��AD�ཻ�ڵ�P����AB=2��BC=4�� 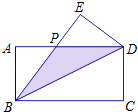
��1��BD=��
��2����P��BD�ľ����� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪Բ���ĵ���뾶Ϊ3cm��ĸ�߳�Ϊ5cm����Բ���IJ�����ǣ� ��
A.30cm2
B.30��cm2
C.15cm2
D.15��cm2
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com