
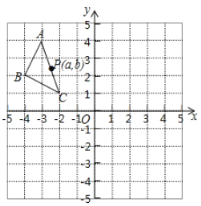
【题目】如图,在平面直角坐标系中,![]() 的三个顶点坐标为
的三个顶点坐标为![]() ,
,![]() ,
,![]() ,
,![]() 绕原点逆时针旋转
绕原点逆时针旋转![]() ,得到
,得到![]() ,
,![]() 向右平移6个单位,再向上平移2个单位得到
向右平移6个单位,再向上平移2个单位得到![]() .
.
(1)画出![]() 和
和![]() ;
;
(2)![]() 是
是![]() 的
的![]() 边上一点,
边上一点,![]() 经旋转、平移后点
经旋转、平移后点![]() 的对应点分别为
的对应点分别为![]() 、
、![]() ,请写出点
,请写出点![]() 、
、![]() 的坐标.
的坐标.
科目:初中数学 来源: 题型:
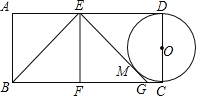
【题目】如图,在矩形ABCD中,AB=4,AD=8,点E、点F分别在边AD,BC上,且EF⊥AD,点B关于EF的对称点为G点,连接EG,若EG与以CD为直径的⊙O恰好相切于点M,则AE的长度为( )
A.3B.![]() C.6+
C.6+![]() D.6﹣
D.6﹣![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
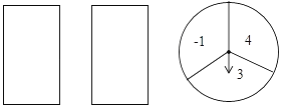
【题目】小红玩抽卡片和旋转盘游戏,有两张正面分别标有数字1,﹣2的不透明卡片,背面完全相同;转盘被平均分成3个相等的扇形,并分别标有数字﹣1,3,4(如图所示),小云把卡片背面朝上洗匀后从中随机抽出一张,记下卡片上的数字;然后转动转盘,转盘停止后,记下指针所在区域的数字(若指针在分格线上,则重转一次,直到指针指向某一区域为止).请用列表或树状图的方法(只选其中一种)求出两个数字之积为负数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】北中环桥是省城太原的一座跨汾河大桥(如图1),它由五个高度不同,跨径也不同的抛物线型钢拱通过吊桥,拉锁与主梁相连,最高的钢拱如图2所示,此钢拱(近似看成二次函数的图象-抛物线)在同一竖直平面内,与拱脚所在的水平面相交于A,B两点,拱高为78米(即最高点O到AB的距离为78米),跨径为90米(即AB=90米),以最高点O为坐标原点,以平行于AB的直线为![]() 轴建立平面直角坐标系,则此抛物线钢拱的函数表达式为( )
轴建立平面直角坐标系,则此抛物线钢拱的函数表达式为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读下列材料,并完成相应的任务.
人类会作圆并且真正了解圆的性质是在2000多年前,由我国的墨子给出圆的概念:“一中同长也.”.意思说,圆有一个圆心,圆心到圆周的长都相等.这个定义比希腊数学家欧几里得给圆下的定义要早100年.与圆有关的定理有很多,弦切角定理就是其中之一.
我们把顶点在圆上,一边和圆相交,另一边和圆相切的角叫做弦切角.
弦切角定理:弦切角的度数等于它所夹弧所对的圆周角度数.
下面是弦切角定理的部分证明过程:
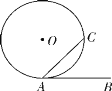
证明:如图①,AB与⊙O相切于点A.当圆心O在弦AC上时,容易得到∠CAB=90°,所以弦切角∠BAC的度数等于它所夹半圆所对的圆周角度数.
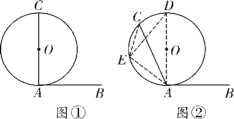
如图②,AB与⊙O相切于点A,当圆心O在∠BAC的内部时,过点A作直径AD交⊙O于点D,在![]() 上任取一点E,连接EC,ED,EA,则∠CED=∠CAD.
上任取一点E,连接EC,ED,EA,则∠CED=∠CAD.
…
任务:
(1)请按照上面的证明思路,写出该证明的剩余部分;
(2)如图③,AB与⊙O相切于点A.当圆心O在∠BAC的外部时,请写出弦切角定理的证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大学毕业生小王响应国家“自主创业”的号召,利用银行小额无息贷款开办了一家饰品店.该店购进一种今年新上市的饰品进行销售,饰品的进价为每件40元,售价为每件60元时,每月可卖出300件.市场调查反映:调整价格时,售价每涨1元每月要少卖10件;售价每下降1元每月要多卖20件.为了获得更大的利润,现将饰品售价调整为x(元/件),每月饰品销量为y(件),月利润为w(元).
(1)直接写出y与x之间的函数关系式;
(2)如何确定售价才能使月利润最大?求最大月利润;
(3)为了使每月利润不少于6000元应如何控制售价?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】元旦期间,某超市销售两种不同品牌的苹果,已知1千克甲种苹果和1千克乙种苹果的进价之和为18元.当销售1千克甲种苹果和1千克乙种苹果利润分别为4元和2元时,陈老师购买3千克甲种苹果和4千克乙种苹果共用82元.
(1)求甲、乙两种苹果的进价分别是每千克多少元?
(2)在(1)的情况下,超市平均每天可售出甲种苹果100千克和乙种苹果140千克,若将这两种苹果的售价各提高1元,则超市每天这两种苹果均少售出10千克,超市决定把这两种苹果的售价提高x元,在不考虑其他因素的条件下,使超市销售这两种苹果共获利960元,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
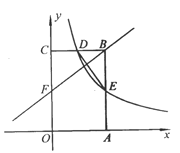
【题目】如图,矩形OABC的顶点A、C分别在x轴和y轴上,点B的坐标为(2,4),双曲线![]() 的图像经过BC的中点D,且与AB交于点E,连接DE.
的图像经过BC的中点D,且与AB交于点E,连接DE.
(1)求k的值及点E的坐标;
(2)若点F是边上一点,且△FBC∽△DEB,求直线FB的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,楼房BD的前方竖立着旗杆AC.小亮在B处观察旗杆顶端C的仰角为45°,在D处观察旗杆顶端C的俯角为30°,楼高BD为20米.
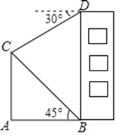
(1)求∠BCD的度数;
(2)求旗杆AC的高度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com