
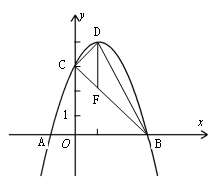
 轴,交直线BC于点F,求线段DF的长,并求△BCD的面积;
轴,交直线BC于点F,求线段DF的长,并求△BCD的面积;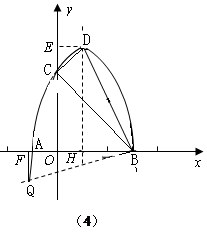
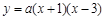
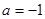 ,
,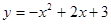 -----------------------2分
-----------------------2分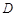 的坐标为(1,4)-----------------------2分
的坐标为(1,4)-----------------------2分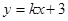 ,把B(3,0)代入,
,把B(3,0)代入,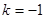 ,所以
,所以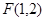
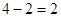 -----------------------2分
-----------------------2分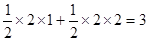 --------------2分
--------------2分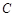 即在抛物线上,CD=
即在抛物线上,CD=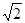 ,BC=
,BC=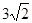 ,
,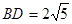 。
。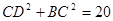 ,
,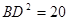 ,∴
,∴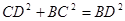 ∴
∴ ,
,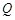 与
与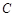 点重合点
点重合点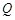 坐标为
坐标为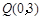 ----------------------------------2分
----------------------------------2分 为
为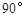 ,作QF⊥
,作QF⊥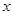 轴于
轴于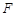 ,
,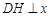 轴于
轴于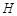
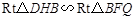
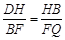
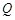 坐标
坐标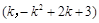
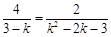

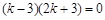
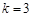 或
或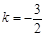
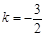 得
得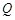 坐标:
坐标: ----------2分
----------2分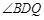 为
为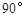
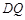 交
交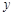 轴于
轴于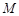 ,
,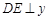 轴于
轴于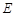 ,
,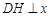 轴于
轴于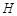
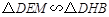
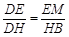
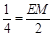
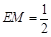 ,
,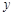 轴交DE于点G,∴
轴交DE于点G,∴
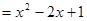 ,
,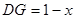 ,
,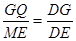 ,
, 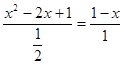 ,解得
,解得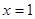 (舍去)
(舍去)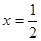 ,
,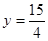 ,
,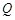 为
为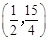
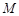 的坐标为
的坐标为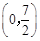
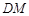 所在的直线方程为
所在的直线方程为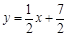
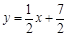 与
与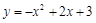 的解为
的解为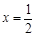 ,得交点坐标
,得交点坐标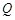 为
为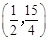 ···················· 2分
···················· 2分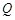 点有三个,
点有三个,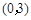 ,
,

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:不详 题型:解答题
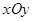 中,点
中,点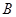 的坐标为
的坐标为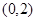 ,点
,点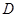 在
在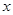 轴的正半轴上,
轴的正半轴上,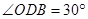 ,
,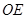 为△
为△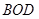 的中线,过
的中线,过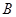 、
、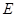 两点的抛物线
两点的抛物线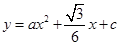 与
与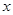 轴相交于
轴相交于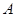 、
、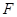 两点(
两点(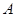 在
在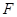 的左侧).
的左侧).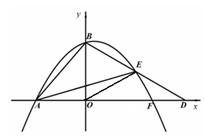
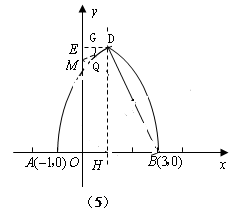
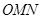 的顶点
的顶点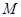 、
、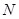 在线段
在线段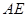 上,求
上,求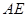 及
及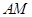 的长;
的长;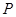 为△
为△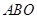 内的一个动点,设
内的一个动点,设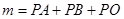 ,请直接写出
,请直接写出 的最小值,以及
的最小值,以及 取得最小值时,线段
取得最小值时,线段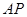 的长.
的长.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
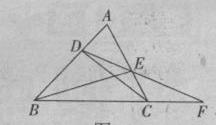
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
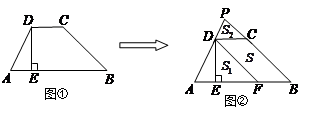
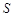 ,△ADF的面积
,△ADF的面积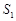 ,△PDC的面积
,△PDC的面积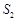 .
.
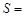 ,
,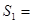 ______,
______,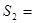 ;
;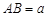 ,
,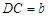 ,
,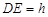 ,则
,则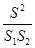 =__________,并写出理由;
=__________,并写出理由;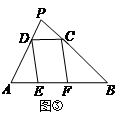
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

| | PA | PQ |
| 第一次 | | |
| 第二次 | | |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 (2)在图②中画一个与格点△ABC相似的格点△A2B2C2,且△A2B2C2与△ABC的相似比为2:1.
(2)在图②中画一个与格点△ABC相似的格点△A2B2C2,且△A2B2C2与△ABC的相似比为2:1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com