
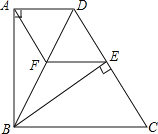
【题目】如图,四边形ABCD中,AD∥BC,BA⊥AD,BC=DC,BE⊥CD于点E.
(1)求证:△ABD≌△EBD;
(2)过点E作EF∥DA,交BD于点F,连接AF.求证:四边形AFED是菱形.
【答案】(1)△ABD≌△EBD;(2)四边形AFED是菱形.
【解析】试题分析:(1)首先证明∠1=∠2.再由BA⊥AD,BE⊥CD可得∠BAD=∠BED=90°,然后再加上公共边BD=BD可得△ABD≌△EBD;
(2)首先证明四边形AFED是平行四边形,再有AD=ED,可得四边形AFED是菱形.
试题解析:证明:(1)如图,
∵AD∥BC,
∴∠1=∠DBC.
∵BC=DC,
∴∠2=∠DBC.
∴∠1=∠2.
∵BA⊥AD,BE⊥CD
∴∠BAD=∠BED=90°,
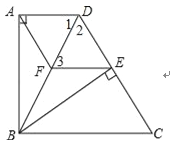
在△ABD和△EBD中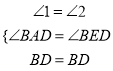 ,
,
∴△ABD≌△EBD(AAS);
(2)由(1)得,AD=ED,∠1=∠2.
∵EF∥DA,
∴∠1=∠3.
∴∠2=∠3.
∴EF=ED.
∴EF=AD.
∴四边形AFED是平行四边形.
又∵AD=ED,
∴四边形AFED是菱形.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:
【题目】已知△ABC与△DEF全等,BC=EF=4cm,△ABC的面积是12cm2 , 则EF边上的高是( )
A. 3cm B. 4cm C. 6cm D. 无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
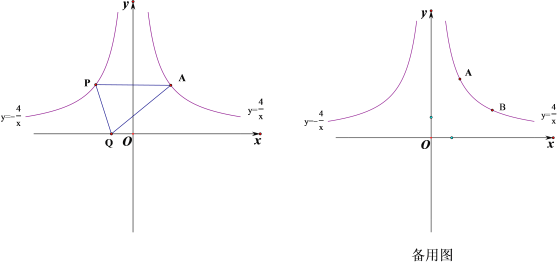
【题目】平面直角坐标系xOy中,已知函数y1=![]() (x>0)与y2=﹣
(x>0)与y2=﹣![]() (x<0)的图象如图所示,点A、B是函数y1=
(x<0)的图象如图所示,点A、B是函数y1=![]() (x>0)图象上的两点,点P是y2=﹣
(x>0)图象上的两点,点P是y2=﹣![]() (x<0)的图象上的一点,且AP∥x轴,点Q是x轴上一点,设点A、B的横坐标分别为m、n(m≠n).
(x<0)的图象上的一点,且AP∥x轴,点Q是x轴上一点,设点A、B的横坐标分别为m、n(m≠n).
(1)求△APQ的面积;
(2)若△APQ是等腰直角三角形,求点Q的坐标;
(3)若△OAB是以AB为底的等腰三角形,求mn的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从M地到N地有一条普通公路,总路程为120km;有一条高速公路,总路程为126km.甲车和乙车同时从M地开往N地,甲车全程走普通公路,乙车先行驶了另一段普通公路,然后再上高速公路.假设两车在普通公路和高速公路上分别保持匀速行驶,其中在普通公路上的行车速度为60km/h,在高速公路上的行车速度为100km/h.设两车出发x h时,距N地的路程为y km,图中的线段AB与折线ACD分别表示甲车与乙车的y与x之间的函数关系.
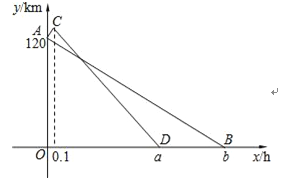
(1)填空:a= ,b= ;
(2)求线段AB、CD所表示的y与x之间的函数关系式;
(3)两车在何时间段内离N地的路程之差达到或超过30km?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:△ABC内接于⊙O,点D在OC的延长线上,sinB=![]() ,∠D=30度.
,∠D=30度.
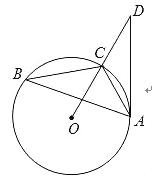
(1)求证:AD是⊙O的切线;
(2)若AC=6,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:
①2a+b=0;
②abc>0;
③方程ax2+bx+c=3有两个相等的实数根;
④抛物线与x轴的另一个交点是(-1,0);
⑤当1<x<4时,有y2<y1,
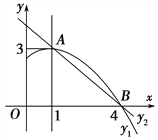
其中正确的是( ).
A. 5个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com