
【题目】如图,在△ABC中,CD⊥AB于点D,AC=4,BC=3,DB=![]() ,
,

(1)、求CD、AD的长
(2)、判断△ABC的形状,并说明理由。
【答案】(1)、CD=![]() ,AD=
,AD=![]() ;(2)、直角三角形,理由见解析
;(2)、直角三角形,理由见解析
【解析】
试题分析:(1)、根据CD⊥AB,BC=3,BD=![]() 得出△CDB和△ADC为直角三角形,然后根据直角三角形的勾股定理分别求出CD和AD的长度;(2)、根据题意得出AC,BC和AB的长度,然后根据勾股定理的逆定理得出三角形为直角三角形.
得出△CDB和△ADC为直角三角形,然后根据直角三角形的勾股定理分别求出CD和AD的长度;(2)、根据题意得出AC,BC和AB的长度,然后根据勾股定理的逆定理得出三角形为直角三角形.
试题解析:(1)、∵CD⊥AB,BC=3,BD=![]() ∴∠CDB=∠CDA=90° ∴在Rt△CDB中,由勾股定理可得:
∴∠CDB=∠CDA=90° ∴在Rt△CDB中,由勾股定理可得:
CD=![]()
在Rt△ADC中,AC=4,CD=![]() ,由勾股定理可得:AD=
,由勾股定理可得:AD=![]() ,
,
△ABC为直角三角形
∵在△ABC中,AC=4,BC=3,AB=AD+BD=![]() +
+![]() =5 ∴
=5 ∴![]()
∴由勾股定理的逆定理可得:△ABC为直角三角形.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】一次数学兴趣小组活动中,同学们做了一个找朋友的游戏:有六个同学A、B、C、D、E、F分别藏在六张大纸牌的后面,如图,A、B、C、D、E、F所持的纸牌的前面分别写有六个算式:66;63+63;(63)3;(2×62)×(3×63);(22×32)3;(64)3÷62.游戏规定:所持算式的值相等的两个人是朋友.如果现在由同学A来找他的朋友,他可以找谁呢?说说你的看法.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A是双曲线![]() 在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为底作等腰△ABC,且∠ACB=120°,点C在第一象限,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线
在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为底作等腰△ABC,且∠ACB=120°,点C在第一象限,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线![]() 上运动,则k的值为( )
上运动,则k的值为( )
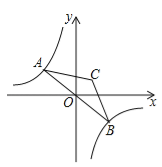
A.1 B.2 C.3 D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com