


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源:不详 题型:解答题
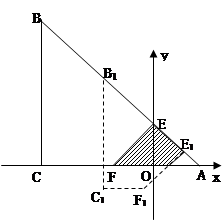
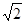 个单位长度从点A沿射线AC运动,试求出当t为何值时,△HE1E为等腰三角形?
个单位长度从点A沿射线AC运动,试求出当t为何值时,△HE1E为等腰三角形?查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
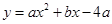 经过
经过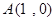 、
、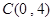 两点,与
两点,与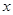 轴交于另一点
轴交于另一点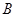 .
.
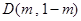 在第二象限的抛物线上,求点
在第二象限的抛物线上,求点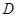 关于直线
关于直线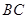 的对称点的坐标;
的对称点的坐标;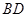 ,点
,点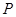 为y轴
为y轴 ,求出点
,求出点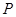 的坐标.
的坐标.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
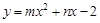 的图象过A(-1,-2)、B(1,0)两点.
的图象过A(-1,-2)、B(1,0)两点.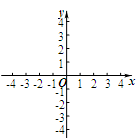
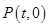 是x轴上的一个动点,过点P作x轴的垂线交直线AB于点M,交二次函数的图象于点N.当点M位于点N的上方时,直接写出t的取值范围.
是x轴上的一个动点,过点P作x轴的垂线交直线AB于点M,交二次函数的图象于点N.当点M位于点N的上方时,直接写出t的取值范围.查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
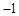 ,0)、(3,0)两点,则下列判断中,错误的是
,0)、(3,0)两点,则下列判断中,错误的是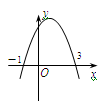
| A.图象的对称轴是直线x=1 |
| B.当x>1时,y随x的增大而减小 |
| C.一元二次方程ax2+bx+c=0的两个根是-1和3 |
| D.当-1<x<3时,y<0 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com