
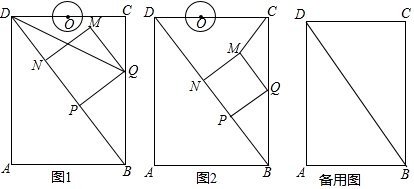
分析 (1)由△DQC≌△DQP,推出DP=DC=6,在Rt△ADB中,BD=$\sqrt{{6}^{2}+{8}^{2}}$=10,推出PB=4即可解决问题.
(2)如图2中,作MT⊥BC于T,由等腰三角形三线合一得:TQ=$\frac{1}{2}$(8-5t),证明△QTM∽△BCD,列比例式得$\frac{QM}{BD}$=$\frac{TQ}{BC}$,代入可得方程,解方程即可;
(3)由题意∠OEF=∠DEN=∠ADB,根据sin∠OEF=sin∠DEN=sin∠ADB=3:5,列出方程即可解决问题.
解答 解:(1)如图1中,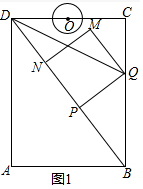
∵∠DQC=∠QDP,QD=QD,∠DCQ=∠DPQ=90°,
∴△DQC≌△DQP,
∴DP=DC=6,
在Rt△ADB中,BD=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∴PB=4,
∴t=1,
故答案为1s;
(2)如图2中,作MT⊥BC于T,
∵MC=MQ,MT⊥CQ,
∴TC=TQ,
由于BP=4t,△ADB∽△PBQ,
∴$\frac{PB}{AD}$=$\frac{PQ}{AB}$,即PQ=$\frac{PB•AB}{AD}$=3t,
∵四边形PQMN为正方形,
∴QM=PQ=3t,
又BQ=$\sqrt{P{B}^{2}+P{Q}^{2}}$=5t
∴TQ=$\frac{1}{2}$(8-5t),
∵MQ∥PN,
∴∠MQT=∠DBC,
∴△QTM∽△BCD,
∴$\frac{QM}{BD}$=$\frac{TQ}{BC}$,即$\frac{3t}{10}$=$\frac{\frac{1}{2}(8-5t)}{8}$,
解得t=$\frac{40}{49}$
∴t=$\frac{40}{49}$s时,△CMQ是以CQ为底的等腰三角形;
(3)设MN与⊙O相切于点F,与CD交于点E,则OF=0.8,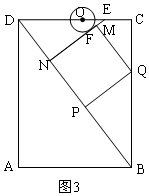
由题意∠OEF=∠DEN=∠ADB,
∴sin∠OEF=sin∠DEN=sin∠ADB=3:5,
∴$\frac{OF}{OE}$=$\frac{3}{5}$,即$\frac{0.8}{OE}$=$\frac{3}{5}$,
∴OE=$\frac{4}{3}$,
当⊙O与直线MN在正方形MNPQ外部相切时,如图3所示,
∵OD=3t,∴DE=3t+$\frac{4}{3}$,
∵BP=4t,NP=PQ=3t,
∴DN=10-7t,
∴$\frac{10-7t}{3t+\frac{4}{3}}$=$\frac{3}{5}$,
∴t=$\frac{23}{22}$,
即当⊙O与直线MN在正方形MNPQ外部相切时,t的值是$\frac{23}{22}$s.
点评 本题考查圆综合题、正方形的性质、相似三角形的判定和性质、切线的判定和性质、勾股定理、角平分线的性质等知识,解题的关键灵活运用这些知识解决问题,学会利用方程的思想思考问题,充分利用相似三角形的性质构建方程,属于中考压轴题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在边长为1个单位长度的小正方形组成的9×9网格中,给出了格点△ABC(顶点是网格线交点),点O在格点上.
如图,在边长为1个单位长度的小正方形组成的9×9网格中,给出了格点△ABC(顶点是网格线交点),点O在格点上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
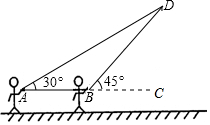 放风筝是大家喜爱的一项体育活动,星期天的上午小刚在市政府广场上放风筝,如图,他在A处不小心让风筝挂在了一棵树梢上,风筝固定在了D处,此时风筝线AD与水平线的夹角为30°,为了便于观察,小刚迅速边收线边向前移动,到达了离A处10米的B处,此时风筝线的长度是多少米?(风筝线AD,BD均为线段,$\sqrt{2}$≈1.414.$\sqrt{3}$≈1.732,最后结果精确到1米)
放风筝是大家喜爱的一项体育活动,星期天的上午小刚在市政府广场上放风筝,如图,他在A处不小心让风筝挂在了一棵树梢上,风筝固定在了D处,此时风筝线AD与水平线的夹角为30°,为了便于观察,小刚迅速边收线边向前移动,到达了离A处10米的B处,此时风筝线的长度是多少米?(风筝线AD,BD均为线段,$\sqrt{2}$≈1.414.$\sqrt{3}$≈1.732,最后结果精确到1米)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
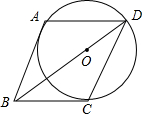 如图,菱形ABCD的顶点A,D,C均在⊙O上,且BC边与⊙O相切于点C.
如图,菱形ABCD的顶点A,D,C均在⊙O上,且BC边与⊙O相切于点C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com