
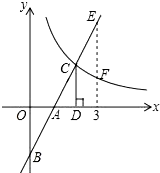
 如图,在直角坐标系中,直线y1=2x-2与坐标轴交于A、B两点,与双曲线y2=$\frac{k}{x}$(x>0)交于点C,过点C作CD⊥x轴,垂足为D,且OA=AD,则以下结论:
如图,在直角坐标系中,直线y1=2x-2与坐标轴交于A、B两点,与双曲线y2=$\frac{k}{x}$(x>0)交于点C,过点C作CD⊥x轴,垂足为D,且OA=AD,则以下结论:分析 由直线y1=2x-2确定出A与B坐标,利用AAS得到三角形OBA与三角形CDA全等,得到CD=OB,确定出C坐标,根据待定系数法确定出反比例解析式,由图象判断y1<y2时x的范围,以及y1与y2的增减性,把x=3分别代入直线与反比例解析式,相减求出EF的长,即可做出判断.
解答 解:对于直线y1=2x-2,
令x=0,得到y=2;令y=0,得到x=1,
∴A(1,0),B(0,-2),即OA=1,OB=2,
在△OBA和△CDA中,
$\left\{\begin{array}{l}{∠AOB=∠ADC=90°}\\{∠OAB=∠DAC}\\{OA=AD}\end{array}\right.$,
∴△OBA≌△CDA(AAS),
∴CD=OB=2,OA=AD=1,
∴S△ADB=S△ADC(同底等高三角形面积相等),选项①正确;
∴C(2,2),
把C坐标代入反比例解析式得:k=4,即y2=$\frac{4}{x}$,
由函数图象得:当0<x<2时,y1<y2,选项②错误;
当x=3时,y1=4,y2=$\frac{4}{3}$,即EF=4-$\frac{4}{3}$=$\frac{8}{3}$,选项③正确;
当x>0时,y1随x的增大而增大,y2随x的增大而减小,选项④正确,
故答案为①③④.
点评 此题考查了反比例函数与一次函数的交点,涉及的知识有:一次函数与坐标系的交点,待定系数法确定反比例函数解析式,坐标与图形性质以及反比例函数的性质,熟练掌握函数的性质是解本题的关键.


 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系xOy中,已知点P(-1,0),C($\sqrt{2}$-1,1),D(0,-3),A,B在x轴上,且P为AB中点,S△CAP=1.
如图,在平面直角坐标系xOy中,已知点P(-1,0),C($\sqrt{2}$-1,1),D(0,-3),A,B在x轴上,且P为AB中点,S△CAP=1.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$÷(-3)=3×(-3) | B. | (-5)÷(-$\frac{1}{2}$)=-5×(-2) | C. | 5-(-2)=5+2 | D. | 2-3=(+2)+(-3) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 学生 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 成绩(个) | 1 | 0 | 2 | -1 | 4 | -2 | 0 | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com