
如图,BD为⊙O的直径,AB=AC,AD交BC于点E.
(1)①求证:△ABE∽△ADB;
②若AE=2,ED=4,求⊙O的面积;
(2)延长DB到F,使得BF=BO,连接FA,若AC∥FD,试判断直线FA与⊙O的位置关系,并说明理由.

(1)①∵⊙O的弦AB=AC,∴弧AB=弧AC,
∴∠ABE=∠ADB,
又∵∠BAE=∠DAB,∴△ABE∽△ADB;
②∵△ABE∽△ADB,
∴ ,可得AB2=AD×AE
,可得AB2=AD×AE
∵AE=2,ED=4,
∴AB2=AD×AE=6×2=12,可得AB=2 ,
,
∵BD为⊙O的直径,
∴Rt△ABD中,BD= =4
=4
所以⊙O的半径为R=2 ,可得⊙O的面积为:S=πR2=12π(平方单位)
,可得⊙O的面积为:S=πR2=12π(平方单位)
(2)直线FA与⊙O相切
证明如下:连接AO

∵AC∥FD,∴∠C=∠CBD
∴弧AC=弧CD,
∵弧AB=弧AC,得弧AC=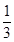 弧BAD
弧BAD
∴∠AOB=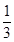 ×180°=60°,
×180°=60°,
可得△ABO是等边三角形.
∴△ABF中,∠FBA=180°-∠ABO=120°
∵BF=BO=AB= BD
BD
∴∠F=∠FBA=30°
因此可得∠FBA+∠BAO=30°+60°=90°
∴OA⊥FA,直线FA过半径OA的外端且与半径OA垂直,
∴直线FA与⊙O相切
【解析】(1)①根据等弧所对的圆周角相等,结合公共角,可得∠ABE=∠ADB且∠BAE=∠DAB,不难得到△ABE∽△ADB;
②由△ABE∽△ADB,可得AB2=AD×AE,代入数据可得AB2=12,结合BD为⊙O的直径,可在Rt△ABD中,求出BD=4 ,从而得到⊙O的半径为2
,从而得到⊙O的半径为2 ,最后利用圆面积公式即得⊙O的面积.
,最后利用圆面积公式即得⊙O的面积.
(2)直线FA与⊙O相切.连接AO,利用平行线的内错角相等,得到∠C=∠CBD,从而弧AC=弧CD,再结合弧AB=弧AC,得到弧AC=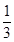 弧BAD,所以∠AOB=60°,得△ABO是等边三角形.接下来不难在等腰△ABF中,算出∠F=∠FBA=30°,因此可得∠FBA+∠BAO=30°+60°=90°,OA⊥FA,得到直线FA与⊙O相切.
弧BAD,所以∠AOB=60°,得△ABO是等边三角形.接下来不难在等腰△ABF中,算出∠F=∠FBA=30°,因此可得∠FBA+∠BAO=30°+60°=90°,OA⊥FA,得到直线FA与⊙O相切.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
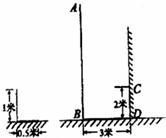 10、如图,一电线杆AB的影子分别落在了地上和墙上,某一时刻,小明竖起1米高的直杆,量得其影长为0.5米,此时,他又量得电线杆AB落在地上的影子BD长3米,落在墙上的影子CD的高为2米.小明用这些数据很快算出了电线杆AB的高.请你计算,电线杆AB的高为( )
10、如图,一电线杆AB的影子分别落在了地上和墙上,某一时刻,小明竖起1米高的直杆,量得其影长为0.5米,此时,他又量得电线杆AB落在地上的影子BD长3米,落在墙上的影子CD的高为2米.小明用这些数据很快算出了电线杆AB的高.请你计算,电线杆AB的高为( )查看答案和解析>>
科目:初中数学 来源: 题型:
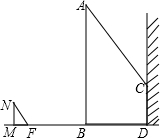 如图,一电线杆AB的影子分别落在了地上和墙上.同一时刻,小明竖起1米高的直杆MN,量得其影长MF为0.5米,量得电线杆AB落在地上的影子BD长3米,落在墙上的影子CD的高为2米.你能利用小明测量的数据算出电线杆AB的高吗?
如图,一电线杆AB的影子分别落在了地上和墙上.同一时刻,小明竖起1米高的直杆MN,量得其影长MF为0.5米,量得电线杆AB落在地上的影子BD长3米,落在墙上的影子CD的高为2米.你能利用小明测量的数据算出电线杆AB的高吗?查看答案和解析>>
科目:初中数学 来源: 题型:
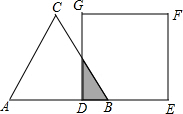 (2012•渝北区一模)如图,等边△ABC的边AB与正方形DEFG的边长均为2,且AB与DE在同一条直线上,开始时点B与点D重合,让△ABC沿这条直线向右平移,直到点B与点E重合为止,设BD的长为x,△ABC与正方形DEFG重叠部分(图中阴影部分)的面积为y,则y与x之间的函数关系的图象大致是( )
(2012•渝北区一模)如图,等边△ABC的边AB与正方形DEFG的边长均为2,且AB与DE在同一条直线上,开始时点B与点D重合,让△ABC沿这条直线向右平移,直到点B与点E重合为止,设BD的长为x,△ABC与正方形DEFG重叠部分(图中阴影部分)的面积为y,则y与x之间的函数关系的图象大致是( )查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
查看答案和解析>>
科目:初中数学 来源:2011届江苏省九年级下册《投影与视图》单元测试数学卷 题型:选择题
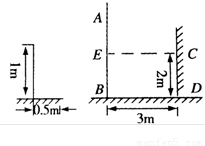
如图,一电线杆AB的影子分别落在地上和墙上,某一时刻,小明竖起1m高的直杆,量
得其影长为0.5m,此时,他又量得电线杆AB落在地上的影子BD长3m,落在墙上的影子
CD的高为2m,小明用这些数据很快算出了电线杆AB的高,请你计算,电线杆AB的高为
( )
A.5m B.6m C.7m D.8m
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com