
 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | ±$\sqrt{2}$ | C. | 2 | D. | ±2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在?ABCD中,过点A作AE⊥BC于点E,AF⊥DC于点F,AE=AF.
如图,在?ABCD中,过点A作AE⊥BC于点E,AF⊥DC于点F,AE=AF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,将一张矩形纸片ABCD沿直线MN折叠,使点C落在点A处,点D落在点E处,直线MN交BC于点M,交AD于点N.
如图,将一张矩形纸片ABCD沿直线MN折叠,使点C落在点A处,点D落在点E处,直线MN交BC于点M,交AD于点N.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
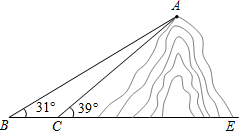 如图,小明想测山高度,他在B处仰望山顶A,测得仰角∠B=31°,再往山的方向(水平方向)前进80m至索道口C处,沿索道方向仰望山顶,测得仰角∠ACE=39°.求这座山的高度(小明的身高忽略不计).
如图,小明想测山高度,他在B处仰望山顶A,测得仰角∠B=31°,再往山的方向(水平方向)前进80m至索道口C处,沿索道方向仰望山顶,测得仰角∠ACE=39°.求这座山的高度(小明的身高忽略不计).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com