
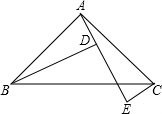
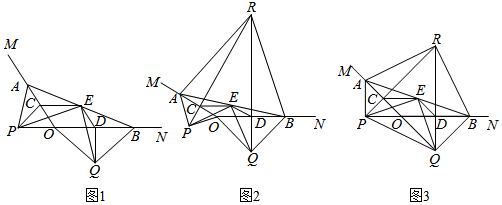
 如图,A、D、E三点在同一直线上,且△BAD≌△ACE,∠ABD=30°,∠ADB=80°.
如图,A、D、E三点在同一直线上,且△BAD≌△ACE,∠ABD=30°,∠ADB=80°.分析 (1)由全等三角形的性质可得∠CAE=∠ABD=30°,∠CEA=∠ADB=80°,利用三角内角和定理可得∠ACE;
(2)由全等三角形的性质可得BD=AE,AD=CE,由AE=AD+DE,等量代换可得BD=DE+CE.
解答 解:(1)∵△BAD≌△ACE,∠ABD=30°,∠ADB=80°,
∴∠CAE=∠ABD=30°,∠CEA=∠ADB=80°,
∴∠ACE=180°-∠CAE-∠CEA=70°;
(2)∵△BAD≌△ACE,
∴BD=AE,AD=CE,
∵AE=AD+DE,
∴AE=CE+DE,
即BD=DE+CE.
点评 本题主要考查了全等三角形的性质定理,熟练掌握定理,运用等量代换是解答此题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
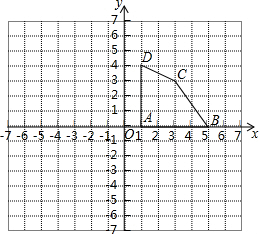 如图,四边形ABCD各顶点的坐标分别为A(1,0),B(5,0),C(3,3),D(1,4).将四边形ABCD先向下平移4个单位长度,再向左平移6个单位长度,得到四边形A′B′C′D′.
如图,四边形ABCD各顶点的坐标分别为A(1,0),B(5,0),C(3,3),D(1,4).将四边形ABCD先向下平移4个单位长度,再向左平移6个单位长度,得到四边形A′B′C′D′.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
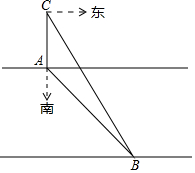 某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的北岸边点A处,测得河的南岸边点B在其南偏东45°方向,然后向北走20米到达C点,测得点B在点C的南偏东33°方向,求出这段河的宽度(结果精确到1米,参考数据sin33°≈0.54,cos33°≈0.84,tan33°≈0.65,$\sqrt{2}$≈1.41)
某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的北岸边点A处,测得河的南岸边点B在其南偏东45°方向,然后向北走20米到达C点,测得点B在点C的南偏东33°方向,求出这段河的宽度(结果精确到1米,参考数据sin33°≈0.54,cos33°≈0.84,tan33°≈0.65,$\sqrt{2}$≈1.41)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
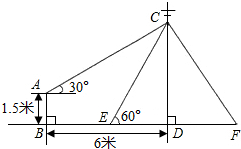 如图,在电线杆上的C处引拉线CE、CF固定电线杆,拉线CE和地面所成的角∠CED=60°,在离电线杆6米的B处安置测角仪AB,在A处测得电线杆上C处的仰角为30°,已知测角仪高AB为1.5米,求拉线CE的长(结果精确到0.1米,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732).
如图,在电线杆上的C处引拉线CE、CF固定电线杆,拉线CE和地面所成的角∠CED=60°,在离电线杆6米的B处安置测角仪AB,在A处测得电线杆上C处的仰角为30°,已知测角仪高AB为1.5米,求拉线CE的长(结果精确到0.1米,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com