
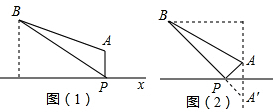
分析 (1)根据勾股定理分别求得S1、S2的值,比较即可;
(2)在公路上任找一点M,连接MA,MB,MA',由轴对称知MA=MA,于是得到MB+MA=MB+MA'>A'B,即可得到S2=BA'为最小.
解答 解:(1)图(1)中过B作BC⊥X于C,垂足为C;AD⊥BC于D,垂足为D,
则BC=40,
又∵AP=10,
∴BD=BC-CD=40-10=30.
在△ABD中,AD=$\sqrt{5{0}^{2}-3{0}^{2}}$=40,
在Rt△PBC中,
∴BP=$\sqrt{C{P}^{2}+B{C}^{2}}$=10$\sqrt{40}$,
S1=40$\sqrt{2}$+10.
图(2)中,过B作BC⊥AA′垂足为C,则A′C=50,
又∵BC=40,
∴BA'=$\sqrt{4{0}^{2}+5{0}^{2}}$=10$\sqrt{41}$,
由轴对称知:PA=PA',
∴S2=BA'=10$\sqrt{41}$,
∴S1>S2.
(2)如图(2),在公路上任找一点M,连接MA,MB,MA',由轴对称知MA=MA',
∴MB+MA=MB+MA'>A'B,
∴S2=BA'为最小.
点评 此题考查了线路最短的问题,确定动点为何位置是关键,综合运用勾股定理的知识.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com