
【题目】某书店现有资金7700元,计划全部用于购进甲、乙、丙三种图书共20套,其中甲种图书每套500元,乙种图书每套400元,丙种图书每套250元.书店将甲、乙、丙三种图书的售价分别定为每套550元,430元,310元.设书店购进甲种图书x套,乙种图书y套,请解答下列问题:
(1)请求出y与x的函数关系式(不需要写出自变量的取值范围);
(2)若书店购进甲、乙两种图书均不少于1套,则该书店有几种进货方案?
(3)在(1)和(2)的条件下,根据市场调查,书店决定将三种图书的售价作如下调整:甲种图书的售价不变,乙种图书的售价上调a(a为正整数)元,丙种图书的售价下调a元,这样三种图书全部售出后,所获得的利润比(2)中某方案的利润多出20元,请直接写出书店是按哪种方案进的货及a的值.
【答案】(1)y=﹣![]() x+18(2)三种购买方案(3)甲种图书6套,乙种图书8套,丙种图书6套,a=10
x+18(2)三种购买方案(3)甲种图书6套,乙种图书8套,丙种图书6套,a=10
【解析】
(1) 根据题意得购进丙种图书(20﹣x﹣y)套,由7700元计划全部用于购进甲、乙、丙三种图书,可列出方程的y与x的函数关系式;
(2)由(1)得:y=﹣![]() x+18,由书店购进甲、乙两种图书均不少于1套,可得
x+18,由书店购进甲、乙两种图书均不少于1套,可得![]() ,得出x的取值范围,由x,y,(20﹣x﹣y)为整数可得方案数;
,得出x的取值范围,由x,y,(20﹣x﹣y)为整数可得方案数;
(3)由(1)(2)得三种方案,按所获得的利润比(2)中某方案的利润多出20元进行比较,由a为正整数进行判断可得出答案.
(1)根据题意得购进丙种图书(20﹣x﹣y)套,则有500x+400y+250(20﹣x﹣y)=7700,
所以解析式为:y=﹣![]() x+18;
x+18;
(2)根据题意得:![]() ,
,
解得:x![]() ,
,
又∵x≥1,
∴![]() ,
,
因为x,y,(20﹣x﹣y)为整数,
∴x=3,6,9,
即有三种购买方案:①甲、乙、丙三种图书分别为3套,13套,4套,
②甲、乙、丙三种图书分别为6套,8套,6套,
③甲、乙、丙三种图书分别为9套,3套,8套,
(3)若按方案一:则有13a﹣4a=20,解得a=![]() (不是正整数,不符合题意),
(不是正整数,不符合题意),
若按方案二:则有8a﹣6a=20,解得a=10(符合题意),
若按方案三:则有3a﹣8a=20,解得a=﹣4(不是正整数,不符合题意),
所以购买方案是:甲种图书6套,乙种图书8套,丙种图书6套,a=10.


科目:初中数学 来源: 题型:
【题目】在日常生活中,观察各种建筑物的地板,就能发现地板常用各种正多边形地砖铺砌成美丽的图案.也就是说,使用给定的某些正多边形,能够拼成一个平面图形,既不留下空隙,又不互相重叠(在几何里叫作平面镶嵌).这显然与正多边形的内角大小有关.当围绕一点拼在一起的几个正多边形的内角加在一起恰好组成一个周角(360°)时,就拼成了一个平面图形.
(1)请根据下列图形,填写表中空格.

(2)如图所示,如果限于用一种正多边形镶嵌,哪几种正多边形能镶嵌成一个平面图形.
(3)不能用正五边形形状的材料铺满地面的理由是什么?
(4)从正三角形、正四边形、正六边形中选一种,再在其他正多边形中选一种,请画出用这两种不同的正多边形镶嵌成的一个平面图形(草图);并探索这两种正多边形共能镶嵌成几种不同的平面图形?说明你的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为6的正三角形纸片ABC按如下顺序进行两次折叠,展开后,得折痕AD、BE.(如图①),点O为其交点.如图②,若P、N分别为BE、BC上的动点.如图③,若点Q在线段BO上,BQ=1,则QN+NP+PD的最小值=_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,∠B=∠C=90°,AB=3,BC=4,CD=1.以AD为腰作等腰△ADE,使∠ADE=90°,过点E作EF⊥DC交直线CD于点F.请画出图形,并直接写出AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
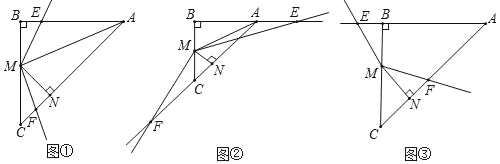
【题目】在等腰△ABC中,∠B=90°,AM是△ABC的角平分线,过点M作MN⊥AC于点N,∠EMF=135°.将∠EMF绕点M旋转,使∠EMF的两边交直线AB于点E,交直线AC于点F,请解答下列问题:
(1)当∠EMF绕点M旋转到如图①的位置时,求证:BE+CF=BM;
(2)当∠EMF绕点M旋转到如图②,图③的位置时,请分别写出线段BE,CF,BM之间的数量关系,不需要证明;
(3)在(1)和(2)的条件下,tan∠BEM=![]() ,AN=
,AN=![]() +1,则BM= ,CF= .
+1,则BM= ,CF= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一项工程,乙队单独完成比甲队单独完成需多用16天,甲队单独做3天的工作量乙队单独做需要5天才能完成.
(1)甲,乙两队单独完成此项工程各需几天?
(2)该项工程先由甲,乙两队合作,再由甲队单独完成,若完成此项工程不超过18天,甲乙两队至少合作几天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出下列4个命题:①两边及其中一边上的中线对应相等的两个三角形全等;②两边及其中一边上的高对应相等的两个三角形全等;③两边及一角对应相等的两个三角形全等;④有两角及其中一角的角平分线对应相等的两个三角形全等.其中正确的的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】材料阅读:
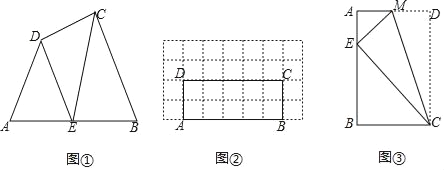
如图①,在四边形ABCD的边AB上任取一点E(点E不与点A、点B重合),分别连接ED,EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的相似点;如果这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的强相似点.
解决问题:
(1)图①中,若∠A=∠B=∠DEC=40°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由;
(2)如图②,在矩形ABCD中,AB=5,BC=2,且A,B,C,D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图②中画出矩形ABCD的边AB上的强相似点(无需写解答过程);
(3)如图③所示的矩形ABCD,将矩形ABCD沿CM折叠后,点D落在AB边上的点E处,若点E恰好是四边形ABCM的边AB上的一个强相似点,试探究点E的位置.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电脑经销商计划购进一批电脑机箱和液晶显示器,若购电脑机箱10台和液液晶显示器8台,共需要资金7000元;若购进电脑机箱2台和液示器5台,共需要资金4120元.
(1)每台电脑机箱、液晶显示器的进价各是多少元?
(2)该经销商购进这两种商品共50台,而可用于购买这两种商品的资金不超过22240元.根据市场行情,销售电脑机箱、液晶显示器一台分别可获利10元和160元.该经销商希望销售完这两种商品,所获利润不少于4100元.试问:该经销商有哪几种进货方案?哪种方案获利最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com