

 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源:不详 题型:解答题
 方向航行10km至B港,再沿北偏西
方向航行10km至B港,再沿北偏西 方向航行10km到达C港.
方向航行10km到达C港. (1)求A、C两港之间的距离(精确到1km)
(1)求A、C两港之间的距离(精确到1km)查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 AD⊥BC,垂足为D,AE∥BC, DE∥AB.
AD⊥BC,垂足为D,AE∥BC, DE∥AB.
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题


查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.1个 | B.2个 | C.3个 | D.4个 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

| A.(2 a+3)cm | B.(2 a+6)cm |
| C.(2a+3)cm | D.(a+6)cm |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.40 | B.30 | C.20 | D.10 |

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

 AB,
AB, CD,连接AF,CE(如图5),则四边形AECF的面积是 ;
CD,连接AF,CE(如图5),则四边形AECF的面积是 ; ABCD的面积是2,AB=a,BC=b,点E从点A出发沿AB以每秒v个单位长的速度向点B运动,点F从点B出发沿BC以每秒
ABCD的面积是2,AB=a,BC=b,点E从点A出发沿AB以每秒v个单位长的速度向点B运动,点F从点B出发沿BC以每秒 个单位长的速度向点C运动.E、F分别从点A、B同时出发,当其中一点到达端点时,另一点也随之停止运动.请问四边形DEBF的面积的值是否随着时间t的变化而变化?若不变,请写出这个值 ,并写出理由;若变化,说明是怎样变化的.
个单位长的速度向点C运动.E、F分别从点A、B同时出发,当其中一点到达端点时,另一点也随之停止运动.请问四边形DEBF的面积的值是否随着时间t的变化而变化?若不变,请写出这个值 ,并写出理由;若变化,说明是怎样变化的.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 与AD重合,由旋转可得:
与AD重合,由旋转可得: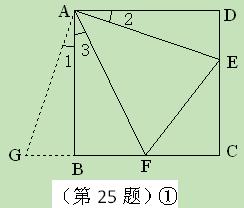
 沿斜边翻折得到△ADC,点E,F分别为DC,BC边上的点,且∠EAF=
沿斜边翻折得到△ADC,点E,F分别为DC,BC边上的点,且∠EAF=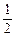 ∠DAB.试猜想DE,BF,EF之间有何数量
∠DAB.试猜想DE,BF,EF之间有何数量 关系,并证明你的猜想.
关系,并证明你的猜想.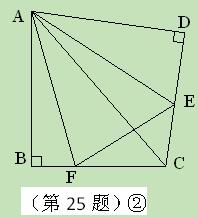
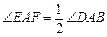 ,试猜想当∠B与∠D满足什么关系时,可使得DE+BF=EF.请直接写出你的猜想(不必说明理由).
,试猜想当∠B与∠D满足什么关系时,可使得DE+BF=EF.请直接写出你的猜想(不必说明理由).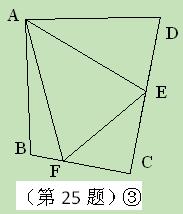
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com