
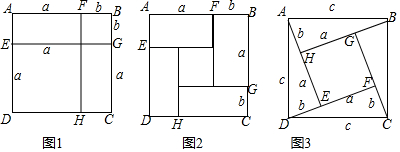
���� ��1������������ABCD�����=��a+b��2��������ABCD�������a-b��2+4ab�����ɵó���a+b��2=��a-b��2+4ab���ݴ˿ɵ�x-y��ֵ��
��2������������ABCD�����=c2��������ABCD�������a-b��2+4��$\frac{1}{2}$ab�����ɵó�a2+b2=c2���ݴ˿ɵù���x��y�ķ����飬���x��y��ֵ��
��� �⣺��1����ͼ2��������ABCD�����=��a+b��2��
������ABCD�������a-b��2+4ab��
�ࣨa+b��2=��a-b��2+4ab��
�ߣ�x+y��2=��x-y��2+4xy����x+y=7��xy=6��
��49=��x-y��2+24��
����x-y��2=25��
��x-y��ֵΪ��5��
�ʴ�Ϊ����a+b��2=��a-b��2+4ab��
��2����ͼ3��������ABCD�����=c2��
������ABCD�������a-b��2+4��$\frac{1}{2}$ab��
��c2=��a-b��2+4��$\frac{1}{2}$ab��
��a2+b2=c2��
�ߵ�a2=3x��b2=$\frac{10}{3}$yʱ��c=4����a2=$\frac{3}{2}$x��b2=2yʱ��c=3��
��$\left\{\begin{array}{l}{3x+\frac{10}{3}y=16}\\{\frac{3}{2}x+2y=9}\end{array}\right.$��
���$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$��
�ʴ�Ϊ��a2+b2=c2��
���� ������Ҫ��������ȫƽ����ʽ�ļ��α����Լ����Ԫһ�η����飬�������Ĺؼ�������������ó���ȫƽ����ʽ����a+b��2=a2+2ab+b2������ʱע�����ν��˼������ã�


 Сѧ�̲�ȫ��ϵ�д�
Сѧ�̲�ȫ��ϵ�д� Сѧ��ѧ������ѿڶ���ϵ�д�
Сѧ��ѧ������ѿڶ���ϵ�д� ������Ӧ�������������ϵ�д�
������Ӧ�������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com