
【题目】小强与小刚都住在安康小区,在同一所学校读书.某天早上,小强![]() 从安康小区站乘坐校车去学校,途中需停靠两个站点才能到达学校站点,且每个站点停留
从安康小区站乘坐校车去学校,途中需停靠两个站点才能到达学校站点,且每个站点停留![]() 分钟,校车行驶途中始终保持匀速.当天早上,小刚
分钟,校车行驶途中始终保持匀速.当天早上,小刚![]() 从安康小区站乘坐出租车沿相同路线出发,出租车匀速行驶,比小强乘坐的校车早
从安康小区站乘坐出租车沿相同路线出发,出租车匀速行驶,比小强乘坐的校车早![]() 分钟到学校站点.他们乘坐的车辆从安康小区站出发所行驶路程
分钟到学校站点.他们乘坐的车辆从安康小区站出发所行驶路程![]() (千米)与行驶时间
(千米)与行驶时间![]() (分钟)之间的函数图象如图所示.
(分钟)之间的函数图象如图所示.
(1)求点![]() 的纵坐标
的纵坐标![]() 的值;
的值;
(2)小刚乘坐出租车出发后经过多少分钟追到小强所乘坐的校车?并求此时他们距学校站点的路程.

科目:初中数学 来源: 题型:
【题目】若二次函数y=ax2+bx+c(a≠0)的图象于x轴的交点坐标分别为(x1 , 0),(x2 , 0),且x1<x2 , 图象上有一点M(x0 , y0)在x轴下方,对于以下说法: ①b2﹣4ac>0;
②x=x0是方程ax2+bx+c=y0的解;
③x1<x0<x2
④a(x0﹣x1)(x0﹣x2)<0;
⑤x0<x1或x0>x2 ,
其中正确的有( )
A.①②
B.①②④
C.①②⑤
D.①②④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,已知A(2,2)、B(4,0).若在坐标轴上取点C,使△ABC为等腰三角形,则满足条件的点C的个数是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
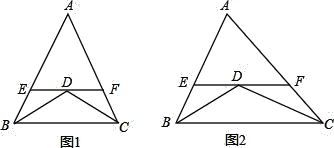
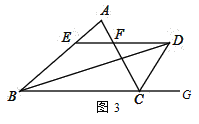
【题目】(1)如图1,已知:在△ABC中,AB=AC=10,BD平分∠ABC,CD平分∠ACB,过点D作EF∥BC,分别交AB、AC于E、F两点,则图中共有__________个等腰三角形;EF与BE、CF之间的数量关系是__________,△AEF的周长是__________;
(2)如图2,若将(1)中“△ABC中,AB=AC=10”该为“若△ABC为不等边三角形,AB=8,AC=10”其余条件不变,则图中共有__________个等腰三角形;EF与BE、CF之间的数量关系是什么?证明你的结论,并求出△AEF的周长;
(3)已知:如图3,D在△ABC外,AB>AC,且BD平分∠ABC,CD平分△ABC的外角∠ACG,过点D作DE∥BC,分别交AB、AC于E、F两点,则EF与BE、CF之间又有何数量关系呢?直接写出结论不证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】任何一个正整数n都可以写成两个正整数相乘的形式,对于两个因数的差的绝对值最小的一种分解a=m×n(m≤n)可称为正整数a的最佳分解,并记作F(a)= ![]() .如:12=1×12=2×6=3×4,则F(12)=
.如:12=1×12=2×6=3×4,则F(12)= ![]() .则在以下结论:
.则在以下结论:
①F(5)=5;②F(24)= ![]() ;
;
③若a是一个完全平方数,则F(a)=1;
④若a是一个完全立方数,即a=x3(x是正整数),
则F(a)=x.则正确的结论有________(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】化简,求值
(1)5x2y+{xy﹣[5x2y﹣(7xy2+![]() xy)]﹣(4x2y+xy)}﹣7xy2,其中x=﹣
xy)]﹣(4x2y+xy)}﹣7xy2,其中x=﹣![]() ,y=﹣16.
,y=﹣16.
(2)A=4x2﹣2xy+4y2,B=3x2﹣6xy+3y2,且|x|=3,y2=16,|x+y|=1,求4A+[(2A﹣B)﹣3(A+B)]的值.
(3)如果m﹣3n+4=0,求:(m﹣3n)2+7m3﹣3(2m3n﹣m2n﹣1)+3(m3+2m3n﹣m2n+n)﹣m﹣10m3的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】认真阅读下面关于三角形内外角平分线的研究片断,完成所提出的问题.
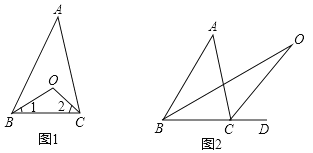
探究1:如图(1)在△ABC中,O是∠ABC与∠ACB的平分线BO和CO的交点,通过分析发现∠BOC=90°+![]() ∠A,理由如下:
∠A,理由如下:
∵BO和CO分别是∠ABC和∠ACB的角平分线,∴∠1=![]() ∠ABC,∠2=
∠ABC,∠2=![]() ∠ACB.
∠ACB.
∴∠1+∠2=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)= ![]() (180°-∠A)=90°-
(180°-∠A)=90°-![]() ∠A.
∠A.
∴∠BOC=180°-(∠1+∠2)=180°-(90°-![]() ∠A)=90°+
∠A)=90°+![]() ∠A
∠A
探究2:如图(2)中,O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y=kx+b经过点A(0,6),且平行于直线y=-2x.
(1)求该函数的解析式,并画出它的图象;
(2)如果这条直线经过点P(m,2),求m的值;
(3)若O为坐标原点,求直线OP的解析式;
(4)求直线y=kx+b和直线OP与坐标轴所围成的图形的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com