
【题目】观察下面一列数,探究其中的规律:—1,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
(1)填空:第11,12,13三个数分别是 , , ;
(2)第2020个数是什么?
(3)如果这列数无限排列下去,与哪个数越来越近?
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)
;(2)![]() ;(3)0.
;(3)0.
【解析】
(1)把1等价于 ![]() ,经观察发现每一项的分子分别是1,分母等于各自的序号,如分母分别是1,2,3,4,5,6…,又知奇数项是负数,偶数项是正数,所以第11,12,13个数分别是-
,经观察发现每一项的分子分别是1,分母等于各自的序号,如分母分别是1,2,3,4,5,6…,又知奇数项是负数,偶数项是正数,所以第11,12,13个数分别是-![]() ,
,![]() ,-
,-![]() ;
;
(2)由(1)的分析可知第2020个数是 ![]() ;
;
(3)分子为1,分母越大,越接近0.
(1)将1等价于![]() ,即:
,即:![]() ,
, ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
可以发现分子永远为1,分母等于序数,奇数项为负数,偶数项为正,由此可以推出第11,12,13个数分别是![]() ,
,![]() ,
,![]() ;
;
(2)第n个数是(1)n![]() ,
,
所以第2020个数为:(1)2020 ![]() ;
;
(3)如果这列数无限排列下去,与0越来越近。
故答案为:(1)![]() ,
,![]() ,
,![]() ;(2)
;(2)![]() ;(3)0.
;(3)0.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
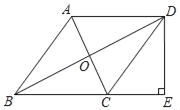
【题目】如图,O为△ABC边AC的中点,AD∥BC交BO的延长线于点D,连接DC,DB平分∠ADC,作DE⊥BC,垂足为E.
(1)求证:四边形ABCD为菱形;
(2)若BD=8,AC=6,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景区一电瓶小客车接到任务从景区大门出发,向东走2千米到达A景区,继续向东走2.5千米到达B景区,然后又回头向西走8.5千米到达C景区,最后回到景区大门.
![]()
(1)以景区大门为原点,向东为正方向,以1个单位长表示1千米,建立如图所示的数轴,请在数轴上表示出上述A、B、C三个景区的位置.
(2)A景区与C景区之间的距离是多少?
(3)若电瓶车充足一次电能行走15千米,则该电瓶车能否在一开始充足电而途中不充电的情况下完成此次任务?请计算说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形![]() 中,点
中,点![]() 为
为![]() 上一点,连接
上一点,连接![]() ,把
,把![]() 沿
沿![]() 折叠得到
折叠得到![]() ,延长
,延长![]() 交
交![]() 于
于![]() ,连接
,连接![]() .
.
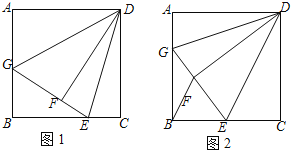
(1)求![]() 的度数.
的度数.
(2)如图![]() ,
,![]() 为
为![]() 的中点,连接
的中点,连接![]() .
.
①求证:![]() ;
;
②若正方形边长为![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“直角”在初中数学学习中无处不在在数学活动课上,李老师要求同学们用所学知识,利用无刻度的直尺和圆规判断“已知∠AOB“是不是直角.甲、乙两名同学各自给出不同的作法,来判断∠AOB是不是直角
甲:如图1,在OA、OB上分别取点CD,以C为圆心,CD长为半径画弧,交OB的反向延长线于点E,若OE=OD,则∠AOB=90°;
乙:如图2,在OA、OB上分别截取OM=4个单位长度,ON=3个单位长度,若MN=5个单位长度,则∠AOB=90°;
甲、乙两位同学作法正确的是( )
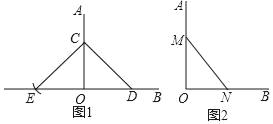
A. 甲正确,乙不正确B. 乙正确,甲不正确
C. 甲和乙都不正确D. 甲和乙都正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为3的正方形OABC的两边在两坐标轴上,抛物线y=-x2+bx+c经过点A,C,与x轴交于另一点D,P为第一象限内抛物线上一点,过P点作y轴的平行线交x 轴于点Q,交AC于点E.
(1)求抛物线解析式及点D的坐标;
(2)过E点作x轴的平行线交AB于点F,若以P,E,F为顶点的三角形与△ODC相似,求点P坐标;
(3)过P点作PH⊥AC于H,是否存在点P使△PEH的周长取得最大值,若存在,请求出点P坐标及△PEH周长的最大值,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下面的知识,后解答后面的问题:
探究:如图,在△ABC中,已知∠B=∠C,求证:AB=AC.

证明:过点A作AD⊥BC,垂足为D, 在△ABD与△ACD中,
∠B=∠C, , , 所以△ABD≌△ACD( ),所以AB=AC.
(1)完成上述证明中的空白;
(2)已知如图,在△ABC中,AC=BC,∠ACB=90°,AD平分∠CAB.试问:AC+CD与AB相等吗?说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数y=![]() (k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH=
(k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH=![]() ,点B的坐标为(m,-2).
,点B的坐标为(m,-2).
(1)求△AHO的周长;
(2)求该反比例函数和一次函数的解析式.

【答案】(1)△AHO的周长为12;(2) 反比例函数的解析式为y=![]() ,一次函数的解析式为y=-
,一次函数的解析式为y=-![]() x+1.
x+1.
【解析】试题分析: (1)根据正切函数,可得AH的长,根据勾股定理,可得AO的长,根据三角形的周长,可得答案;
(2)根据待定系数法,可得函数解析式.
试题解析:(1)由OH=3,tan∠AOH=![]() ,得
,得
AH=4.即A(-4,3).
由勾股定理,得
AO=![]() =5,
=5,
△AHO的周长=AO+AH+OH=3+4+5=12;
(2)将A点坐标代入y=![]() (k≠0),得
(k≠0),得
k=-4×3=-12,
反比例函数的解析式为y=![]() ;
;
当y=-2时,-2=![]() ,解得x=6,即B(6,-2).
,解得x=6,即B(6,-2).
将A、B点坐标代入y=ax+b,得
![]() ,
,
解得 ,
,
一次函数的解析式为y=-![]() x+1.
x+1.
考点:反比例函数与一次函数的交点问题.
【题型】解答题
【结束】
25
【题目】如图,已知点A、C分别在∠GBE的边BG、BE上,且AB=AC,AD∥BE,∠GBE的平分线与AD交于点D,连接CD.
求证:①AB=AD;
②CD平分∠ACE.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com