练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
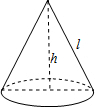
    20．如图是一顶圆锥形烟囱小纸帽，它的母线长l是13cm，高h为12cm，则制作这顶纸帽所需纸张的面积是（接缝忽略不计）（　　）
    A．60πB．65πC．78πD．156π

    分析 根据勾股定理求得圆锥的底面半径，然后利用圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长和扇形面积公式计算即可．

    解答 解：∵圆锥的母线长l是13cm，高h为12cm，
    ∴圆锥的底面半径为r=$\sqrt{1{3}^{2}-1{2}^{2}}$=5cm，
    ∴这张扇形纸板的面积=$\frac{1}{2}$×2π×5×13=65π（cm2）．
    故选B．

    点评 本题考查了圆锥的计算：圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    10．如图，抛物线y=ax2-5ax-6a交x轴于A、B两点（A左B右），交y轴于点C，直线y=-x+b交抛物线于D，交x轴于E，且△ACE的面积为6．
    （1）求抛物线的解析式；
    （2）点P为CD上方抛物线上一点，过点P作x轴的平行线，交直线CD于F，设P点的横坐标为m，线段PF的长为d，求d与m的函数关系式；
    （3）在（2）的条件下，过点P作PG⊥CD，垂足为G，若∠APG=∠ACO，求点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

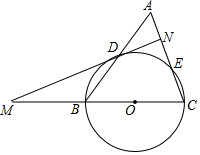    11．如图，△ABC中，AC=BC=a，AB=b，以BC为直径作⊙O交AB于点D，交AC于点E，过点D作⊙O的切线MN，交CB的延长线于点M，交AC于点N．
    （1）求证：MN⊥AC；
    （2）连接BE，写出求BE长的思路．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．如图，某校教学楼AB的后面有一办公楼CD，当光线与地面的夹角是22°时，教学楼在建筑物的墙上留下高3米的影子CE；而当光线与地面的夹角是45°时，教学楼顶A在地面上的影子F与墙角C有30米的距离（B、F、C在一条直线上）．现要在A、E之间挂一些彩旗，求A、E之间的距离．（参考数据：sin22°≈$\frac{3}{8}$，cos22°≈$\frac{15}{16}$，tan22°≈$\frac{2}{5}$，精确到0.1m）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．如图，数轴上有A、B、C、D四个点，其中所对应的数的绝对值最大的点是（　　）
    A．点AB．点BC．点CD．点D

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．定义：在平行四边形中，若有一条对角线是一边得两倍，则称这个平行四边形为两倍四边形，其中这条对角线叫做两倍对角线，这条边叫做两倍边．
    如图1，四边形ABCD是平行四边形，BE∥AC，延长DC交BE于点E，连结AE交BC于点F，AB=1，AD=m．
    （1）若∠ABC=90°，如图2．
    ①当m=2时，试说明四边形ABEC是两倍四边形；
    ②是否存在值m，使得四边形ABCD是两倍四边形，若存在，求出m的值，若不存在，请说明理由；
    （2）如图1，四边形ABCD与四边形ABEC都是两倍四边形，其中BD与AE为两倍对角线，AD与AC为两倍边，求m的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．问题背景：课外学习小组在一次学习研讨中，得到了如下两个命题：
    ①如图1，在等边三角形ABC中，M、N分别是AC、AB上的点，BM与CN相交于点O，若∠BON=60°，则BM=CN．
    ②如图2，在正方形ABCD中，M、N分别是CD、AD上的点，BM与CN相交于点O，若∠BON=90°，则BM=CN．
    任务要求：
    （1）请你从①、②两个命题中选择一个进行证明．
    （2）请你继续完成下面的探索：
    ①如图3，在正n（n≥3）边形ABCDEF…中，M，N分别是CD，DE上的点，BM与CN相交于点O，试问当∠BON等于多少度时，结论BM=CN成立；（不要求证明）
    ②如图4，在正五边形ABCDE中，M，N分别是DE，AE上的点，BM与CN相交于点O，若∠BON=108°时，试问结论BM=CN是否还成立．若成立，请给予证明；若不成立，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．关于x的一元二次方程ax2+2x+c=0（a≠0）有两个相等的实数根，写出一组满足条件的实数a，c的值：a=1，c=1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

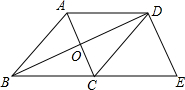    10．如图，在菱形ABCD中，对角线AC与BD相交于点O，过点D作DE⊥BD交BC的延长线于点E．
    （1）求证：四边形ACED是平行四边形；
    （2）若BD=4，AC=3，求cos∠CDE的值．

    查看答案和解析>>

    同步练习册答案