
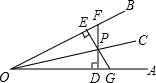
 如图,P是∠AOB的平分线OC上的一点,PD⊥OA,PE⊥OB,垂足分别为D,E,延长DP交OB于点F,延长EP交OA于点G,则图中有三对全等三角形,它们分别是Rt△POE和Rt△POD、△PEF和△PDG、△POF和△POG.
如图,P是∠AOB的平分线OC上的一点,PD⊥OA,PE⊥OB,垂足分别为D,E,延长DP交OB于点F,延长EP交OA于点G,则图中有三对全等三角形,它们分别是Rt△POE和Rt△POD、△PEF和△PDG、△POF和△POG. 分析 由角平分线的性质可得PE=PD,可证明△POE≌△OOD,△PEF≌△PDG,进一步可证明△POF≌△POG,可得出答案.
解答 解:
∵P是∠AOB的平分线OC上的一点,PD⊥OA,PE⊥OB,
∴PE=PD,
在Rt△POE和Rt△POD中
$\left\{\begin{array}{l}{PE=PD}\\{OP=OP}\end{array}\right.$
∴R△POE≌Rt△POD(HL),
在△PEF和△PDG中
$\left\{\begin{array}{l}{∠PEF=∠PDG}\\{PE=PD}\\{∠EPF=∠DPG}\end{array}\right.$
∴△PEF≌△PDG(ASA),
∴∠OFP=∠OGP,
在△POF和△POG中
$\left\{\begin{array}{l}{∠POF=∠POG}\\{∠OFP=∠OGP}\\{OP=OP}\end{array}\right.$
∴△POF≌△POG(AAS),
∴全等的三角形有三对,它们分别是Rt△POE和Rt△POD、△PEF和△PDG、△POF和△POG,
故答案为:三;Rt△POE和Rt△POD、△PEF和△PDG、△POF和△POG.
点评 本题主要考查全等三角形的判定,掌握全等三角形的判定方法是解题的关键,即SSS、SAS、ASA、AAS和HL.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
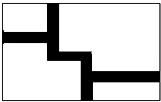 如图,在长为32 米,宽为20 米的矩形地面上修建同样宽度的道路(图中阴影部分),余下的部分种植草坪,要使草坪的面积为540m2,求道路的宽是多少米?
如图,在长为32 米,宽为20 米的矩形地面上修建同样宽度的道路(图中阴影部分),余下的部分种植草坪,要使草坪的面积为540m2,求道路的宽是多少米?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (a-b)2=a2-b2 | B. | (a+2b)2=a2+2ab+b2 | C. | (a+b)2=a2+b2 | D. | (-a+b)2=a2-2ab+b2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com