
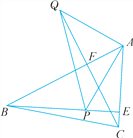
【题目】如图,已知在△ABC中,AB>AC,BE,CF都是△ABC的高线,P是BE上一点,且BP=AC,Q是CF延长线上一点,且CQ=AB,连结AP,AQ,QP.求证:
(1)AQ=PA.
(2)AP⊥AQ.
【答案】(1)证明见解析(2)证明见解析
【解析】试题分析:(1)由已知条件可求出∠ABP=∠QCA,即可根据SAS证得△AQC≌△PAB(SAS),就可以得出AP=AQ;
(2)根据全等三角形的性质,由△AQC≌△PAB可得出∠BAP=∠CQA,再由∠CQA+∠FAQ=90°,即可证明.
试题解析:(1)∵BE,CF是△ABC的高线,
∴BE⊥AC,CF⊥AB,
∴∠ABP+∠BAC=∠ACQ+∠BAC=90°,
∴∠ABP=∠ACQ.
在△AQC和△PAB中,∵ 
∴△AQC≌△PAB(SAS).∴AQ=PA.
(2)∵△AQC≌△PAB,∴∠BAP=∠CQA.
∵∠CQA+∠BAQ=90°,
∴∠BAP+∠BAQ=90°,∴AP⊥AQ.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:
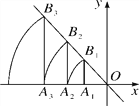
【题目】如图,直线l:y=-![]() x,点A1的坐标为(-3,0).过点A1作x轴的垂线交直线l于点B1,以原点O为圆心,OB1长为半径画弧交x轴负半轴于点A2,再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交x轴负半轴于点A3,则点A3的坐标为________,按此作法进行下去,点A2017的坐标为__________.
x,点A1的坐标为(-3,0).过点A1作x轴的垂线交直线l于点B1,以原点O为圆心,OB1长为半径画弧交x轴负半轴于点A2,再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交x轴负半轴于点A3,则点A3的坐标为________,按此作法进行下去,点A2017的坐标为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△DCE都是直角三角形,其中一个三角形是由另一个三角形旋转得到的,下列叙述中错误的是( ) 
A.旋转中心是点C
B.顺时针旋转角是90°
C.旋转中心是点B,旋转角是∠ABC
D.既可以是逆时针旋转又可以是顺时针旋转
查看答案和解析>>
科目:初中数学 来源: 题型:
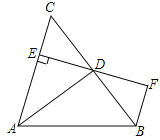
【题目】(3分)如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有( )
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
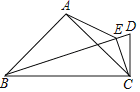
【题目】如图,等腰直角△ABC中,∠BAC=90°,BC=6,过点C作CD⊥BC,CD=2,连接BD,过点C作CE⊥BD,垂足为E,连接AE,则AE长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A. 为了了解东北地区初中生每天体育锻炼的时间,应采用普查的方式
B. 平均数相同的甲、乙两组数据,若甲组数据的方差![]() ,乙组数据的方差
,乙组数据的方差![]() ,则乙组数据比甲组数据稳定
,则乙组数据比甲组数据稳定
C. 掷一枚质地均匀的硬币![]() 次,必有
次,必有![]() 次正面朝上
次正面朝上
D. 数据![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的中位数是
的中位数是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)36﹣76+(﹣23)﹣(﹣10)
(2)﹣6﹣9
(3)(﹣1![]() )﹣(+6
)﹣(+6![]() )﹣2.25+
)﹣2.25+![]()
(4)11+(﹣35)﹣(﹣41)+(﹣16)
(5)(﹣3![]() )﹣(﹣2
)﹣(﹣2![]() )﹣(﹣1
)﹣(﹣1![]() )﹣(+1.75)
)﹣(+1.75)
(6)(﹣4![]() )﹣(﹣5
)﹣(﹣5![]() )+(﹣4
)+(﹣4![]() )﹣(+3
)﹣(+3![]() ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com