
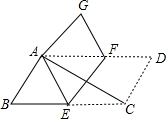
 如图,将平行四边形ABCD纸片沿EF折叠,使点C与点A重合,点D落在点G处,
如图,将平行四边形ABCD纸片沿EF折叠,使点C与点A重合,点D落在点G处,分析 (1)利用全等三角形的判定得出△AOF≌△COE(ASA),证得EO=FO,进而根据平行四边形的判定证得四边形AECF是平行四边形,因为AC⊥EF,即可证得四边形AECF是菱形;
(2)根据?ABCD与菱形AECF同高,$\frac{EC}{BC}=\frac{2}{3}$,进而得出?ABCD与菱形AECF的面积,进而根据菱形的面积等于两对角线乘积的一半即可得出答案.
解答 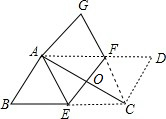 (1)证明:∵将?ABCD纸片沿EF折叠,使点C与点A重合,
(1)证明:∵将?ABCD纸片沿EF折叠,使点C与点A重合,
∴AO=CO,∠AOF=∠COE=90°,AD=BC,FG=DF,
在△AOF和△COE中.
$\left\{\begin{array}{l}{∠FAO=∠ECO}\\{AO=CO}\\{∠AOF=∠COE}\end{array}\right.$,
∴△AOF≌△COE(ASA),
∴EO=FO,
∵AO=CO,
∴四边形AECF是平行四边形,
∵AC⊥EF,
∴平行四边形AECF是菱形,
(2)解:∵?ABCD与菱形AECF同高,$\frac{EC}{BC}=\frac{2}{3}$,
∴?ABCD与菱形AECF的面积的比为:3:2,
∵平行四边形ABCD的面积为8,
∴菱形AECF的面积为$\frac{16}{3}$,
∵AC⊥EF,
∴菱形AECF的面积为:$\frac{1}{2}$×AC×EF=$\frac{16}{3}$,
∴AC•EF=$\frac{32}{3}$.
点评 此题主要考查了菱形的判定以及平行四边形的性质和全等三角形的判定与性质等知识,得出△AOF≌△COE是解题关键.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
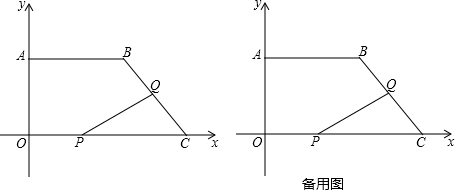
 如图,已知△ABC、△DCE、△FEG是三个全等的等腰三角形,底边BC、CE、EG在同一直线上,且AB=$\sqrt{3}$,BC=1.连接BF,分别交AC、DC、DE与点P、Q、R.有下列结论①△BFG∽△ABC、②BQ=FQ、③AP=2PC、④EF平分∠BFG,你认为不正确的是④.
如图,已知△ABC、△DCE、△FEG是三个全等的等腰三角形,底边BC、CE、EG在同一直线上,且AB=$\sqrt{3}$,BC=1.连接BF,分别交AC、DC、DE与点P、Q、R.有下列结论①△BFG∽△ABC、②BQ=FQ、③AP=2PC、④EF平分∠BFG,你认为不正确的是④.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
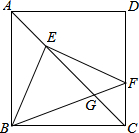 如图,已知,正方形ABCD的边长为1,点E、F分别在AC、DC上,若EC=BC,EF⊥BE,BF与EC交于G,则BG与GF的乘积为$3\sqrt{2}-4$.
如图,已知,正方形ABCD的边长为1,点E、F分别在AC、DC上,若EC=BC,EF⊥BE,BF与EC交于G,则BG与GF的乘积为$3\sqrt{2}-4$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com