
【题目】已知关于x的一元二次方程:2x2+6x﹣a=0.
(1)当a=5时,解方程;
(2)若2x2+6x﹣a=0的一个解是x=1,求a;
(3)若2x2+6x﹣a=0无实数解,试确定a的取值范围.
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,点E是平面内异于点A的任意一点,以线段AE为边作正方形AEFG,连接EB,GD.
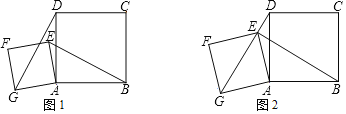
(1)如图1,求证EB=GD;
(2)如图2,若点E在线段DG上,AB=5,AG=3![]() ,求BE的长.
,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“一带一路”倡议提出五年多来,交通、通信、能源等各项相关建设取得积极进展,也为增进各国民众福祉提供了新的发展机遇.下图是2017年“一年一路”沿线部分国家的通信设施现状统计图.
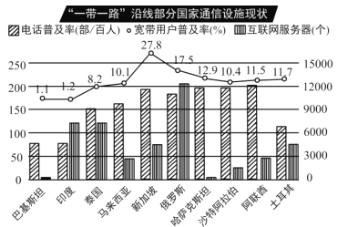
根据统计图提供的信息,下列推断合理的是( ).
A.互联网服务器拥有个数最多的国家是阿联酋
B.宽带用户普及率的中位数是11.05%
C.有8个国家的电话普及率能够达到平均每人1部
D.只有俄罗斯的三项指标均超过了相应的中位数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是等边三角形ABC内一点,且PA=3,PB=4, PC=5,若将△APB绕着点B逆时针旋转后得到△CQB,则∠APB的度数______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=![]() x2+
x2+![]() x+4与x轴相交于点A、B与y轴相交于点C,抛物线的对称轴与x轴相交于点M,P是抛物线在x轴下方的一个动点(点P、M、C不在同一条直线上).分别过点A、B作直线CP的垂线,垂足分别为D、E,连接点MD、ME.
x+4与x轴相交于点A、B与y轴相交于点C,抛物线的对称轴与x轴相交于点M,P是抛物线在x轴下方的一个动点(点P、M、C不在同一条直线上).分别过点A、B作直线CP的垂线,垂足分别为D、E,连接点MD、ME.
(1)写出点A,B的坐标, 并证明△MDE是等腰三角形;
(2)△MDE能否为等腰直角三角形?若能,求此时点的坐标;若不能,说明理由;
(3)若将“P是抛物线在x轴下方的一个动点(点P、M、C不在同一条直线上)”改为“P是抛物线在x轴上方的一个动点”,其他条件不变,△MDE能否为等腰直角三角形?若能求此时点P的坐标(直接写出结果);若不能,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
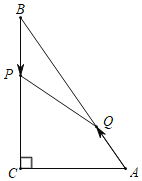
【题目】如图,在Rt△ABC中,∠C=90°,AC=6cm,BC=8cm.点P从B出发,沿BC方向,以1cm/s的速度向点C运动,点Q从A出发,沿AB方向,以2cm/s的速度向点B运动;若两点同时出发,当其中一点到达端点时,两点同时停止运动,设运动时间为t(s)(t>0),△BPQ的面积为S(cm2).
(1)t=2秒时,则点P到AB的距离是 cm,S= cm2;
(2)t为何值时,PQ⊥AB;
(3)t为何值时,△BPQ是以BP为底边的等腰三角形;
(4)求S与t之间的函数关系式,并求S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知抛物线y=x2-2mx-3m
(1)当m=1时,
①抛物线的对称轴为直线______,
②抛物线上一点P到x轴的距离为4,求点P的坐标
③当n≤x≤![]() 时,函数值y的取值范围是-
时,函数值y的取值范围是-![]() ≤y≤2-n,求n的值
≤y≤2-n,求n的值
(2)设抛物线y=x2-2mx-3m在2m-1≤x≤2m+1上最低点的纵坐标为y0,直接写出y0与m之间的函数关系式及m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]()
![]() 过点
过点![]() ,顶点为M点.
,顶点为M点.

(1)求该抛物线的解析式;
(2)试判断抛物线上是否存在一点P,使∠POM=90.若不存在,说明理由;若存在,求出P点的坐标;
(3)试判断抛物线上是否存在一点K,使∠OMK=90,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B、C三个城市位置如图所示,A城在B城正南方向180 km处,C城在B城南偏东37°方向.已知一列货车从A城出发匀速驶往B城,同时一辆客车从B城出发匀速驶往C城,出发1小时后,货车到达P地,客车到达M地,此时测得∠BPM=26°,两车又继续行驶1小时,货车到达Q地,客车到达N地,此时测得∠BNQ=45°,求两车的速度.(参考数据:sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tan37°≈
,tan37°≈![]() ,sin26°≈
,sin26°≈![]() ,cos26°≈
,cos26°≈![]() ,tan26°≈
,tan26°≈![]() )
)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com