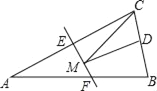
【题目】如图：等腰△ABC的底边BC长为6，面积是18，腰AC的垂直平分线EF分别交AC，AB边于E，F点．若点D为BC边的中点，点M为线段EF上一动点，则△CDM周长的最小值为（ ）
A. 6 B. 8 C. 9 D. 10
【答案】C
【解析】
连接AD，AM，由于△ABC是等腰三角形，点D是BC边的中点，故AD⊥BC，再根据三角形的面积公式求出AD的长，再根据EF是线段AC的垂直平分线可知，点A关于直线EF的对称点为点C，MA＝MC，推出MC+DM＝MA+DM≥AD，故AD的长为BM+MD的最小值，由此即可得出结论．
连接AD，MA．
∵△ABC是等腰三角形，点D是BC边的中点，∴AD⊥BC，∴S△ABC
BCAD
6×AD＝18，解得：AD＝6．
∵EF是线段AC的垂直平分线，∴点A关于直线EF的对称点为点C，MA＝MC，∴MC+DM＝MA+DM≥AD，∴AD的长为CM+MD的最小值，∴△CDM的周长最短＝（CM+MD）+CD＝AD
BC＝6
6＝6+3＝9．
故选C．
夺冠训练单元期末冲刺100分系列答案
新思维小冠军100分作业本系列答案科目：初中数学 来源： 题型：
【题目】已知，⊙O的两条弦AB、CD相交于点E，
（1）如图1，若BE=DE，求证： 
= 
； 
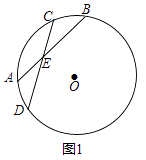
（2）如图2，在（1）的条件下，连接OC，AP为⊙O的直径，PQ为⊙O的弦，且PQ∥AB，求证：∠OCD=∠APQ； 
（3）如图3，在（2）的条件下，连接BD分别与OA、OC交于点G、H，连接DQ，设CD与AP交于点F， 若PQ=2CF，BH=5GH，DQ=4，求⊙O的半径．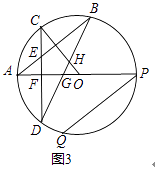
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】把一根绳子对折成一条线段AB，在线段AB取一点P，使AP＝
，从P处把绳子剪断，若剪断后的三段绳子中最长的一段为30cm，则绳子的原长为______cm．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC中，AB＝AC，∠BAC＝90°，点D是直线AB上的一动点（不和A、B重合），BE⊥CD于E，交直线AC于F．
（1）点D在边AB上时，请证明：BD＝AB﹣AF；
（2）试探索：点D在AB的延长线或反向延长线上时，请在备用图中画出图形，（1）中的结论是否成立？若不成立，请直接写出正确结论（不需要证明）．
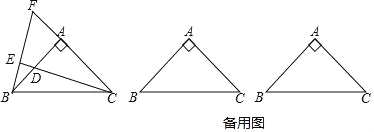
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AB＝AC，CD垂直AB于D，P为BC上的任意一点，过P点分别作PE⊥AB，PF⊥CA，垂足分别为E，F．
（1）若P为BC边中点，则PE，PF，CD三条线段有何数量关系（写出推理过程）？
（2）若P为线段BC上任意一点，则（1）中关系还成立吗？
（3）若P为直线BC上任意一点，则PE，PF，CD三条线段间有何数量关系（请直接写出）．
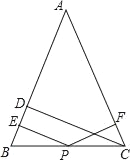
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】两个全等的三角尺重叠摆放在△ACB的位置，将其中一个三角尺绕着点C按逆时针方向旋转到△DCE的位置，使点A恰好落在边DE上，AB与 CE相交于点F．已知∠ACB＝∠DCE＝90°，∠B＝30°，AB＝16cm，则AF＝____．
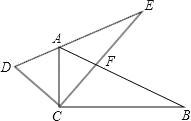
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC中，分别延长△ABC的边AB、AC到D、E，∠CBD与∠BCE的平分线相交于点P，爱动脑筋的小明在写作业的时发现如下规律：
(1)若∠A＝60°，则∠P＝ °；
(2)若∠A＝40°，则∠P＝ °；
(3)若∠A＝100°，则∠P＝ °；
(4)请你用数学表达式归纳∠A与∠P的关系 ．
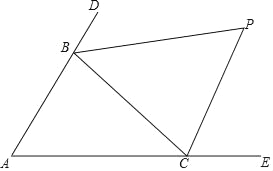
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知锐角三角形ABC，以点A为圆心，AC为半径画弧与BC交于点E，分别以点E、C为圆心，以大于 
EC的长为半径画弧相交于点P，作射线AP，交BC于点D．若BC=5，AD=4，tan∠BAD= 
，则AC的长为（ ）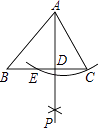 
A.3
B.5
C.
D.2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
