
ЁОЬтФПЁПЙлВьВТЯыЃКЃЈ1ЃЉШчЭМЂйЃЌдкRtЁїABCжаЃЌЁЯBACЃН90ЁуЃЌABЃНACЃН3ЃЌЕуDгыЕуAжиКЯЃЌЕуEдкБпBCЩЯЃЌСЌНгDEЃЌНЋЯпЖЮDEШЦЕуDЫГЪБеыа§зЊ90ЁуЕУЕНЯпЖЮDFЃЌСЌНгBFЃЌBEгыBFЕФЮЛжУЙиЯЕЪЧЁЁ ЁЁЃЌBE+BFЃНЁЁ ЁЁЃЛ
ЬНОПжЄУїЃКЃЈ2ЃЉдкЃЈ1ЃЉжаЃЌШчЙћНЋЕуDбиABЗНЯђвЦЖЏЃЌЪЙADЃН1ЃЌЦфгрЬѕМўВЛБфЃЌШчЭМЂкЃЌХаЖЯBEгыBFЕФЮЛжУЙиЯЕЃЌВЂЧѓBE+BFЕФжЕЃЌЧыаДГіФуЕФРэгЩЛђМЦЫуЙ§ГЬЃЛ
ЭиеЙбгЩьЃКЃЈ3ЃЉШчЭМЂлЃЌдкЁїABCжаЃЌABЃНACЃЌЁЯBACЃНaЃЌЕуDдкБпBAЕФбгГЄЯпЩЯЃЌBDЃНnЃЌСЌНгDEЃЌНЋЯпЖЮDEШЦзХЕуDЫГЪБеыа§зЊЃЌа§зЊНЧЁЯEDFЃНaЃЌСЌНгBFЃЌдђBE+BFЕФжЕЪЧЖрЩйЃПЧыгУКЌгаnЃЌaЕФЪНзгжБНгаДГіНсТлЃЎ
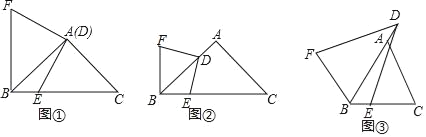
ЁОД№АИЁПЙлВьВТЯыЃКЃЈ1ЃЉBFЁЭBEЃЌBCЃЛЬНОПжЄУїЃКЃЈ2ЃЉBFЁЭBEЃЌBF+BEЃН![]() ЃЌМћНтЮіЃЛЭиеЙбгЩьЃКЃЈ3ЃЉBF+BEЃН
ЃЌМћНтЮіЃЛЭиеЙбгЩьЃКЃЈ3ЃЉBF+BEЃН![]() .
.
ЁОНтЮіЁП
ЃЈ1ЃЉжЛвЊжЄУїЁїBAFЁеЁїCAEЃЌМДПЩНтОіЮЪЬтЃЛ
ЃЈ2ЃЉШчЭМЂкжаЃЌзїDHЁЮACНЛBCгкHЃЎРћгУЃЈ1ЃЉжаНсТлМДПЩНтОіЮЪЬтЃЛ
ЃЈ3ЃЉШчЭМЂлжаЃЌзїDHЁЮACНЛBCЕФбгГЄЯпгкHЃЌзїDMЁЭBCгкMЃЎжЛвЊжЄУїЁїBDFЁеЁїHDEЃЌПЩжЄBF+BEЃНBHЃЌМДПЩНтОіЮЪЬт.
ЃЈ1ЃЉШчЭМЂйжаЃЌ
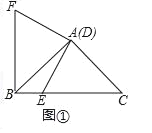
ЁпЁЯEAFЃНЁЯBACЃН90ЁуЃЌ
ЁрЁЯBAFЃНЁЯCAEЃЌ
ЁпAFЃНAEЃЌABЃНACЃЌ
ЁрЁїBAFЁеЁїCAEЃЌ
ЁрЁЯABFЃНЁЯCЃЌBFЃНCEЃЌ
ЁпABЃНACЃЌЁЯBACЃН90ЁуЃЌ
ЁрЁЯABCЃНЁЯCЃН45ЁуЃЌ
ЁрЁЯFBEЃНЁЯABF+ЁЯABCЃН90ЁуЃЌBCЃНBE+ECЃНBE+BFЃЌ
ЙЪД№АИЮЊBFЁЭBEЃЌBCЃЛ
ЃЈ2ЃЉШчЭМЂкжаЃЌзїDHЁЮACНЛBCгкHЃЌ
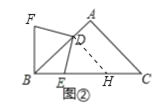
ЁпDHЁЮACЃЌ
ЁрЁЯBDHЃНЁЯAЃН90ЁуЃЌЁїDBHЪЧЕШбќжБНЧШ§НЧаЮЃЌ
гЩЃЈ1ЃЉПЩжЊЃЌBFЁЭBEЃЌBF+BEЃНBHЃЌ
ЁпABЃНACЃН3ЃЌADЃН1ЃЌ
ЁрBDЃНDHЃН2ЃЌ
ЁрBHЃН2![]() ЃЌ
ЃЌ
ЁрBF+BEЃНBHЃН2![]() ЃЛ
ЃЛ
ЃЈ3ЃЉШчЭМЂлжаЃЌзїDHЁЮACНЛBCЕФбгГЄЯпгкHЃЌзїDMЁЭBCгкMЃЌ
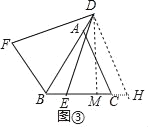
ЁпACЁЮDHЃЌ
ЁрЁЯACHЃНЁЯHЃЌЁЯBDHЃНЁЯBACЃНІСЃЌ
ЁпABЃНACЃЌ
ЁрЁЯABCЃНЁЯACB
ЁрЁЯDBHЃНЁЯHЃЌ
ЁрDBЃНDHЃЌ
ЁпЁЯEDFЃНЁЯBDHЃНІСЃЌ
ЁрЁЯBDFЃНЁЯHDEЃЌ
ЁпDFЃНDEЃЌDBЃНDHЃЌ
ЁрЁїBDFЁеЁїHDEЃЌ
ЁрBFЃНEHЃЌ
ЁрBF+BEЃНEH+BEЃНBHЃЌ
ЁпDBЃНDHЃЌDMЁЭBHЃЌ
ЁрBMЃНMHЃЌЁЯBDMЃНЁЯHDMЃЌ
ЁрBMЃНMHЃНBDsin![]() ЃЎ
ЃЎ
ЁрBF+BEЃНBHЃН2nsin![]() ЃЎ
ЃЎ


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПгаЫФеХНівЛУцЗжБ№Бъга1ЃЌ2ЃЌ3ЃЌ4ЕФВЛЭИУїжНЦЌЃЌГ§ЫљБъЪ§зжВЛЭЌЭтЃЌЦфгрЖМЭъШЋЯрЭЌЃЎ
ЃЈ1ЃЉНЋЫФеХжНЦЌЗжГЩСНзщЃЌБъга1ЁЂ3ЕФЮЊЕквЛзщЃЌБъга2ЁЂ4ЕФЮЊЕкЖўзщЃЌБГУцЯђЩЯЃЌЗХдкзРЩЯЃЌДгСНзщжаИїЫцЛњГщШЁвЛеХЃЌЧѓСНДЮГщШЁЪ§зжКЭЮЊ5ЕФИХТЪЃЛ
ЃЈ2ЃЉНЋЫФеХжНЦЌЯДдШКѓБГУцЯђЩЯЃЌЗХдкзРЩЯЃЌвЛДЮадДгжаЫцЛњГщШЁСНеХЃЌгУЪїаЮЭМЗЈЛђСаБэЗЈЃЌЧѓЫљГщШЁЪ§зжКЭЮЊ5ЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП(1)дФЖСРэНт
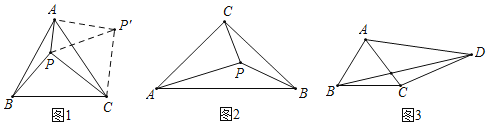
РћгУа§зЊБфЛЛНтОіЪ§бЇЮЪЬтЪЧвЛжжГЃгУЕФЗНЗЈЃЎШчЭМ1ЃЌЕуPЪЧЕШБпШ§НЧаЮABCФквЛЕуЃЌPAЃН1ЃЌPBЃН![]() ЃЌPCЃН2ЃЎЧѓЁЯBPCЕФЖШЪ§ЃЎ
ЃЌPCЃН2ЃЎЧѓЁЯBPCЕФЖШЪ§ЃЎ
ЮЊРћгУвбжЊЬѕМўЃЌВЛЗСАбЁїBPCШЦЕуCЫГЪБеыа§зЊ60ЁуЕУЁїAPЁфCЃЌСЌНгPPЁфЃЌдђPPЁфЕФГЄЮЊ_____ЃЛдкЁїPAPЁфжаЃЌвзжЄЁЯPAPЁфЃН90ЁуЃЌЧвЁЯPPЁфAЕФЖШЪ§ЮЊ_____ЃЌзлЩЯПЩЕУЁЯBPCЕФЖШЪ§ЮЊ_____ЃЛ
(2)РрБШЧЈвЦ
ШчЭМ2ЃЌЕуPЪЧЕШбќRtЁїABCФкЕФвЛЕуЃЌЁЯACBЃН90ЁуЃЌPAЃН2ЃЌPBЃН![]() ЃЌPCЃН1ЃЌЧѓЁЯAPCЕФЖШЪ§ЃЛ
ЃЌPCЃН1ЃЌЧѓЁЯAPCЕФЖШЪ§ЃЛ
(3)ЭиеЙгІгУ
ШчЭМ3ЃЌдкЫФБпаЮABCDжаЃЌBCЃН3ЃЌCDЃН5ЃЌABЃНACЃН![]() ADЃЎЁЯBACЃН2ЁЯADCЃЌЧыжБНгаДГіBDЕФГЄЃЎ
ADЃЎЁЯBACЃН2ЁЯADCЃЌЧыжБНгаДГіBDЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ1ЃЉГЂЪдЬНОП
ШчЭМ1ЃЌЕШбќRtЁїABCЕФСНИіЖЅЕуBЃЌCдкжБЯпMNЩЯЃЌЕуDЪЧжБЯпMNЩЯвЛИіЖЏЕуЃЈЕуDдкЕуCЕФгвБпЃЉЃЌBC=3ЃЌBD=mЃЌдкЁїABCЭЌВрзїЕШбќRtЁїADEЃЌЁЯABC=ЁЯADE=90ЁуЃЌEFЁЭ MNгкЕуFЃЌСЌНсCE.
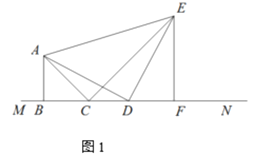
ЂйЧѓDFЕФГЄЃЛ
ЂкдкХаЖЯACЁЭCEЪЧЗёГЩСЂЪБЃЌаЁУїЭЌбЇЗЂЯжПЩвдгЩвдЯТСНжжЫМТЗНтОіДЫЮЪЬтЃК
ЫМТЗвЛЃКЯШжЄCF=EFЃЌЧѓГіЁЯECF=45ЁуЃЌДгЖјжЄЕУНсТлГЩСЂ.
ЫМТЗЖўЃКЯШЧѓDFЃЌEFЕФГЄЃЌдйЧѓCFЕФГЄЃЌШЛКѓжЄAC2+CE2=AE2ЃЌДгЖјжЄЕУНсТлГЩСЂ.
ЧыФуШЮбЁвЛжжЫМТЗЃЌЭъећЕиЪщаДБОаЁЬтЕФжЄУїЙ§ГЬ.(ШчгУСНжжЗНЗЈзїД№ЃЌдђвдЕквЛжжЗНЗЈЦРЗж)
ЃЈ2ЃЉЭиеЙЬНОП
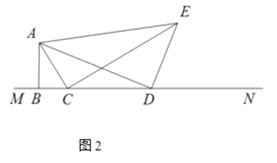
НЋ(1)жаЕФСНИіЕШбќжБНЧШ§НЧаЮЖМИФЮЊгавЛИіНЧЮЊЕФжБНЧШ§НЧаЮЃЌШчЭМ2ЃЌ ЁЯABC=ЁЯADE=90ЁуЃЌЁЯBAC=ЁЯDAE=30ЁуЃЌBC=3ЃЌBD=mЃЌЕБ4ЁмmЁм6ЪБЃЌЧѓCEГЄЕФЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯC=90ЁуЃЌвдACЮЊжБОЖзїЁбOЃЌНЛABгкDЃЌЙ§ЕуOзїOEЁЮABЃЌНЛBCгкEЃЎ
ЃЈ1ЃЉЧѓжЄЃКEDЮЊЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉШчЙћЁбOЕФАыОЖЮЊ![]() ЃЌED=2ЃЌбгГЄEOНЛЁбOгкFЃЌСЌНгDFЁЂAFЃЌЧѓЁїADFЕФУцЛ§ЃЎ
ЃЌED=2ЃЌбгГЄEOНЛЁбOгкFЃЌСЌНгDFЁЂAFЃЌЧѓЁїADFЕФУцЛ§ЃЎ

ЁОД№АИЁПЃЈ1ЃЉжЄУїМћНтЮіЃЛЃЈ2ЃЉ![]()
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉЪзЯШСЌНгODЃЌгЩOEЁЮABЃЌИљОнЦНааЯпгыЕШбќШ§НЧаЮЕФаджЪЃЌвзжЄЕУ![]() Ёе
Ёе![]() МДПЩЕУ
МДПЩЕУ![]() ЃЌдђПЩжЄЕУ
ЃЌдђПЩжЄЕУ![]() ЮЊ
ЮЊ![]() ЕФЧаЯпЃЛ
ЕФЧаЯпЃЛ
ЃЈ2ЃЉСЌНгCDЃЌИљОнжБОЖЫљЖдЕФдВжмНЧЪЧжБНЧЃЌМДПЩЕУ![]() РћгУЙДЙЩЖЈРэМДПЩЧѓЕУ
РћгУЙДЙЩЖЈРэМДПЩЧѓЕУ![]() ЕФГЄЃЌгжгЩOEЁЮABЃЌжЄЕУ
ЕФГЄЃЌгжгЩOEЁЮABЃЌжЄЕУ![]() ИљОнЯрЫЦШ§НЧаЮЕФЖдгІБпГЩБШР§ЃЌМДПЩЧѓЕУ
ИљОнЯрЫЦШ§НЧаЮЕФЖдгІБпГЩБШР§ЃЌМДПЩЧѓЕУ![]() ЕФГЄЃЌШЛКѓРћгУШ§НЧКЏЪ§ЕФжЊЪЖЃЌЧѓЕУ
ЕФГЄЃЌШЛКѓРћгУШ§НЧКЏЪ§ЕФжЊЪЖЃЌЧѓЕУ![]() гы
гы![]() ЕФГЄЃЌШЛКѓРћгУSЁїADF=SЬнаЮABEF-SЬнаЮDBEFЧѓЕУД№АИЃЎ
ЕФГЄЃЌШЛКѓРћгУSЁїADF=SЬнаЮABEF-SЬнаЮDBEFЧѓЕУД№АИЃЎ
ЪдЬтНтЮіЃК(1)жЄУїЃКСЌНгODЃЌ

ЁпOEЁЮABЃЌ
ЁрЁЯCOE=ЁЯCADЃЌЁЯEOD=ЁЯODAЃЌ
ЁпOA=OD,
ЁрЁЯOAD=ЁЯODAЃЌ
ЁрЁЯCOE=ЁЯDOEЃЌ
дкЁїCOEКЭЁїDOEжаЃЌ
 ЁрЁїCOEЁеЁїDOE(SAS)ЃЌ
ЁрЁїCOEЁеЁїDOE(SAS)ЃЌ
![]()
ЁрEDЁЭODЃЌ
ЁрEDЪЧ![]() ЕФЧаЯпЃЛ
ЕФЧаЯпЃЛ
(2)СЌНгCDЃЌНЛOEгкMЃЌ
дкRtЁїODEжаЃЌ
ЁпOD=32ЃЌDE=2ЃЌ
![]()
ЁпOEЁЮABЃЌ
ЁрЁїCOEЁзЁїCABЃЌ
![]() ЁрAB=5ЃЌ
ЁрAB=5ЃЌ
ЁпACЪЧжБОЖЃЌ
![]()
![]()
![]()
![]()
ЁпEFЁЮABЃЌ
![]()
![]()
![]()
ЁрSЁїADF=SЬнаЮABEFSЬнаЮDBEF
![]()
ЁрЁїADFЕФУцЛ§ЮЊ![]()

ЁОЬтаЭЁПНтД№Ьт
ЁОНсЪјЁП
25
ЁОЬтФПЁПЁОЬтФПЁПвбжЊЃЌХзЮяЯпy=ax2+ax+bЃЈaЁй0ЃЉгыжБЯпy=2x+mгавЛИіЙЋЙВЕуMЃЈ1ЃЌ0ЃЉЃЌЧвaЃМbЃЎ
ЃЈ1ЃЉЧѓbгыaЕФЙиЯЕЪНКЭХзЮяЯпЕФЖЅЕуDзјБъЃЈгУaЕФДњЪ§ЪНБэЪОЃЉЃЛ
ЃЈ2ЃЉжБЯпгыХзЮяЯпЕФСэЭтвЛИіНЛЕуМЧЮЊNЃЌЧѓЁїDMNЕФУцЛ§гыaЕФЙиЯЕЪНЃЛ
ЃЈ3ЃЉa=Љ1ЪБЃЌжБЯпy=Љ2xгыХзЮяЯпдкЕкЖўЯѓЯоНЛгкЕуGЃЌЕуGЁЂHЙигкдЕуЖдГЦЃЌЯжНЋЯпЖЮGHбиyжсЯђЩЯЦНвЦtИіЕЅЮЛЃЈtЃО0ЃЉЃЌШєЯпЖЮGHгыХзЮяЯпгаСНИіВЛЭЌЕФЙЋЙВЕуЃЌЪдЧѓtЕФШЁжЕЗЖЮЇЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊ:е§ЗНаЮABCDЃЌЕШбќжБНЧШ§НЧАхЕФжБНЧЖЅЕуТфдке§ЗНаЮЕФЖЅЕуDДІЃЌЪЙШ§НЧАхШЦЕуDа§зЊ.
(1)ЕБШ§НЧАха§зЊЕНЭМ1ЕФЮЛжУЪБЃЌВТЯыCEгыAFЕФЪ§СПЙиЯЕЃЌВЂМгвджЄУїЃЛ
(2)дк(1)ЕФЬѕМўЯТЃЌШєDE:AE:CE= 1: ![]() :3ЃЌЧѓЁЯAEDЕФЖШЪ§ЃЛ
:3ЃЌЧѓЁЯAEDЕФЖШЪ§ЃЛ
(3)ШєBC= 4ЃЌЕуMЪЧБпABЕФжаЕуЃЌСЌНсDMЃЌDMгыACНЛгкЕуOЃЌЕБШ§НЧАхЕФвЛБпDFгыБпDMжиКЯЪБ(ШчЭМ2)ЃЌШєOF=![]() ЃЌЧѓCNЕФГЄ.
ЃЌЧѓCNЕФГЄ.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌЁїABCжаЃЌЁЯAЃН30ЁуЃЌЕуPДгЕуAГіЗЂвд2cm/sЕФЫйЖШбиелЯпAЁњCЁњBдЫЖЏЃЌЕуQДгЕуAГіЗЂвдvcm/sЕФЫйЖШбиABдЫЖЏЃЌPЃЌQСНЕуЭЌЪБГіЗЂЃЌЕБФГвЛЕудЫЖЏЕНЕуBЪБЃЌСНЕуЭЌЪБЭЃжЙдЫЖЏЃЎЩшдЫЖЏЪБМфЮЊxЃЈsЃЉЃЌЁїAPQЕФУцЛ§ЮЊyЃЈcm2ЃЉЃЌyЙигкxЕФКЏЪ§ЭМЯѓгЩC1ЃЌC2СНЖЮзщГЩЃЌШчЭМ2ЫљЪОЃЌгаЯТСаНсТлЃКЂйvЃН1ЃЛЂкsinBЃН![]() ЃЛЂлЭМЯѓC2ЖЮЕФКЏЪ§БэДяЪНЮЊyЃНЉ
ЃЛЂлЭМЯѓC2ЖЮЕФКЏЪ§БэДяЪНЮЊyЃНЉ![]() x2+
x2+![]() xЃЛЂмЁїAPQУцЛ§ЕФзюДѓжЕЮЊ8ЃЌЦфжае§ШЗгаЃЈЁЁЁЁЃЉ
xЃЛЂмЁїAPQУцЛ§ЕФзюДѓжЕЮЊ8ЃЌЦфжае§ШЗгаЃЈЁЁЁЁЃЉ
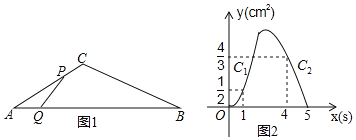
A.ЂйЂкB.ЂйЂкЂмC.ЂйЂлЂмD.ЂйЂкЂлЂм
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
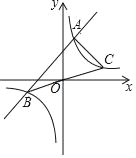
ЁОЬтФПЁПШчЭМЃЌвбжЊКЏЪ§yЃНx+2ЕФЭМЯѓгыКЏЪ§yЃН![]() ЃЈkЁй0ЃЉЕФЭМЯѓНЛгкAЁЂBСНЕуЃЌСЌНгBOВЂбгГЄНЛКЏЪ§yЃН
ЃЈkЁй0ЃЉЕФЭМЯѓНЛгкAЁЂBСНЕуЃЌСЌНгBOВЂбгГЄНЛКЏЪ§yЃН![]() ЃЈkЁй0ЃЉЕФЭМЯѓгкЕуCЃЌСЌНгACЃЌШєЁїABCЕФУцЛ§ЮЊ8ЃЎдђkЕФжЕЮЊ_____ЃЎ
ЃЈkЁй0ЃЉЕФЭМЯѓгкЕуCЃЌСЌНгACЃЌШєЁїABCЕФУцЛ§ЮЊ8ЃЎдђkЕФжЕЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯC=90ЁуЃЌЁЯBACЕФЦНЗжЯпНЛBCгкЕуDЃЌЕуOдкABЩЯЃЌвдЕуOЮЊдВаФЃЌOAЮЊАыОЖЕФдВЧЁКУОЙ§ЕуDЃЌЗжБ№НЛACЃЌABгкЕуEЃЌFЃЎ
ЃЈ1ЃЉЪдХаЖЯжБЯпBCгыЁбOЕФЮЛжУЙиЯЕЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ2ЃЉШєBD=2![]() ЃЌBF=2ЃЌЧѓвѕгАВПЗжЕФУцЛ§ЃЈНсЙћБЃСєІаЃЉЃЎ
ЃЌBF=2ЃЌЧѓвѕгАВПЗжЕФУцЛ§ЃЈНсЙћБЃСєІаЃЉЃЎ

ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com