
【题目】如图,将两块直角三角尺的直角顶点O叠放在一起.
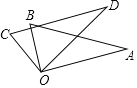
(1)如果∠BOD=60°,那么∠AOC= ,如果∠AOC=130°,那么∠BOD= .
(2)猜想∠AOC与∠BOD的数量关系,并说明理由.
【答案】(1)120°,50°;(2)∠AOC+∠BOD=180°,见解析.
【解析】
(1)根据角的和差即可得到结论;
(2)依据∠AOC=∠BOD+∠AOD+∠BOC求解即可.
解:(1)∵∠AOB=∠COD=90°,
∴∠BOC=90°﹣∠BOD=90°﹣60°=30°,
∴∠AOC=∠AOB+∠BOC=90°+30°=120°,
∵∠AOC=130°,
∴∠BOC=130°﹣90°=40°,
∴∠BOD=90°﹣40°=50°,
故答案为:120°,50°;
(2)∠AOC+∠BOD=180°.
理由如下:∵∠AOB=∠COD=90°,
∴∠AOB+∠COD=180°,
又∵∠AOB=∠AOD+∠BOD,
∵∠COD=∠BOC+∠BOD,
∴∠AOD+∠BOD+∠BOC+∠BOD=180°.
又∵∠BOD+∠AOD+∠BOC=∠AOC,
∴∠AOC+∠BOD=180°.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案科目:初中数学 来源: 题型:
【题目】已知:直线![]() 与x轴、y轴分别相交于点A和点B,点C在线段AO上.将
与x轴、y轴分别相交于点A和点B,点C在线段AO上.将![]() 沿BC折叠后,点O恰好落在AB边上点D处.
沿BC折叠后,点O恰好落在AB边上点D处.
(1)求出OC的长?
(2)点E、F是直线BC上的两点,若![]() 是以EF为斜边的等腰直角三角形,求点F的坐标;
是以EF为斜边的等腰直角三角形,求点F的坐标;
(3)取AB的中点M,若点P在y轴上,点Q在直线AB上,是否存在以C、M、P、Q为顶点的四边形为平行四边形?若存在,请求出所有满足条件的Q点坐标;若不存在,请说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在线段AB上有一点C(点C不与A、B重合且AC>BC),分别以AC、BC为边作正方形ACED和正方形BCFG,其中点F在边CE上,连接AG.

(1)如图1,若AC=7,BC=5,则AG=______;
(2)如图2,若点C是线段AB的三等分点,连接AE、EG,求证:△AEG是直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上点![]() 为原点,点
为原点,点![]() 表示的数为
表示的数为![]() ,点
,点![]() 表示的数为
表示的数为![]() ,且
,且![]() 满足
满足![]()
![]()
(1)![]() 两点对应的数分别为
两点对应的数分别为![]() ______,
______,![]() ______;
______;
(2)若将数轴折叠,使得A点与B点重合,则原点O与数______表示的点重合;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() (k为常数,k≠1).
(k为常数,k≠1).
(1)其图象与正比例函数y=x的图象的一个交点为P.若点P的纵坐标是2,求k的值;
(2)若在其图象的每一支上,y随x的增大而减小,求k的取值范围;
(3)若其图象的一支位于第二象限,在这一支上任取两点A(x1,y1),B(x2,y2),当y1>y2时,试比较x1与x2的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点,点M是AB边上的一个动点(不与点A重合),延长ME交CD的延长线于点N,连接MD,AN.
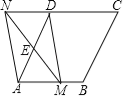
(1)求证:四边形AMDN是平行四边形.
(2)当AM的值为何值时,四边形AMDN是矩形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校需要添置教师办公桌椅A、B两型共200套,已知2套A型桌椅和1套B型桌椅共需2000元,1套A型桌椅和3套B型桌椅共需3000元.
(1)求A,B两型桌椅的单价;
(2)若需要A型桌椅不少于120套,B型桌椅不少于70套,平均每套桌椅需要运费10元.设购买A型桌椅x套时,总费用为y元,求y与x的函数关系式,并直接写出x的取值范围;
(3)求出总费用最少的购置方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解方程:(1) ![]() ; (2)
; (2)![]() .
.
【答案】(1)x1 =1 ,x2=![]() ; (2) x1 =-1,x2=
; (2) x1 =-1,x2=![]() .
.
【解析】试题分析:
根据两方程的特点,使用“因式分解法”解两方程即可.
试题解析:
(1)原方程可化为: ![]() ,
,
方程左边分解因式得: ![]() ,
,
![]() 或
或![]() ,
,
解得: ![]() ,
, ![]() .
.
(2)原方程可化为: ![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() 或
或![]() ,
,
解得: ![]() .
.
【题型】解答题
【结束】
20
【题目】已知x1,x2是关于x的一元二次方程x2-2(m+1)x+m2+5=0的两实根.
(1)若(x1-1)(x2-1)=28,求m的值;
(2)已知等腰△ABC的一边长为7,若x1,x2恰好是△ABC另外两边的边长,求这个三角形的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com