
 已知:如图所示,在四边形ABCD中,E、F分别为AB、CD的中点
已知:如图所示,在四边形ABCD中,E、F分别为AB、CD的中点分析 (1)如图1,取AD的中点G,连接EG,FG,根据三角形的中位线的性质得到EG+FG=$\frac{1}{2}$(BD+AC),根据三角形的三边关系健康得到结论;
(2)①如图2,当AD与BC不平行,取AC的中点H,连接EH,FH,根据三角形中位线的性质得到FH=$\frac{1}{2}$AD,EH=$\frac{1}{2}$BC,根据三角形的三边关系得到EF<$\frac{1}{2}$(AD+BC),②当AD∥BC时,得到EF=$\frac{1}{2}$(AD+BC),于是得到结论;
解答 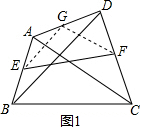 解:(1)如图1,取AD的中点G,连接EG,FG,
解:(1)如图1,取AD的中点G,连接EG,FG,
∵E、F分别为AB、CD的中点,
∴EG,FG分别是△ABD与△ACD的中位线,
∴EG=$\frac{1}{2}$BD,FG=$\frac{1}{2}$AC
∴EG+FG=$\frac{1}{2}$(BD+AC),
在三角形EFG中,∵EF<EG+FG,
∴EF<$\frac{1}{2}$(AC+BD);
(2)①如图2,当AD与BC不平行,取AC的中点H,连接EH,FH,
∵E、F分别为AB、CD的中点,
∴EH,FH分别是△ACD与△ACB的中位线,
∴FH=$\frac{1}{2}$AD,EH=$\frac{1}{2}$BC,
∴FH+EH=$\frac{1}{2}$(AD+BC),
∵EH+FH>EF,
∴EF<$\frac{1}{2}$(AD+BC),
②当AD∥BC时,
E,H,F三点共线,
∴EF=$\frac{1}{2}$(AD+BC),
∴EF≤$\frac{1}{2}$(AD+BC).
点评 本题考查了三角形的中位线的性质,三角形的三边关系,正确的作出辅助线是解题的关键.


科目:初中数学 来源: 题型:解答题
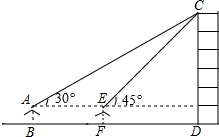 某数学兴趣小组在学习了《锐角三角函数》以后,开展测量物体高度的实践活动,测量一建筑物CD的高度,他们站在B处仰望楼顶C,测得仰角为30°,再往建筑物方向走20m,到达点F处测得楼顶C的仰角为45°(BFD在同一直线上).已知观测员的眼睛与地面距离为1.5m(即AB=1.5m),求这栋建筑物CD的高度.(参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414.结果保留整数)
某数学兴趣小组在学习了《锐角三角函数》以后,开展测量物体高度的实践活动,测量一建筑物CD的高度,他们站在B处仰望楼顶C,测得仰角为30°,再往建筑物方向走20m,到达点F处测得楼顶C的仰角为45°(BFD在同一直线上).已知观测员的眼睛与地面距离为1.5m(即AB=1.5m),求这栋建筑物CD的高度.(参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414.结果保留整数)查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | AC=BD | B. | AC⊥BD | C. | ∠ABD=∠BAC | D. | ∠BAC+∠CAD=90° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com