
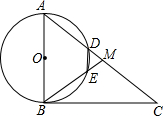
 如图,在Rt△ABC中,∠ABC=90°,点M是AC的中点,以AB为直径作⊙O分别交AC,BM于点D,E.
如图,在Rt△ABC中,∠ABC=90°,点M是AC的中点,以AB为直径作⊙O分别交AC,BM于点D,E.分析 (1)先证明∠A=∠ABM,再证明∠MDE=∠MBA,∠MED=∠A即可解决问题.
(2)①由DE∥AB,得$\frac{DE}{AB}$=$\frac{MD}{MA}$即可解决问题.
②当∠A=60°时,四边形ODME是菱形,只要证明△ODE,△DEM都是等边三角形即可.
解答 (1)证明:∵∠ABC=90°,AM=MC,
∴BM=AM=MC,
∴∠A=∠ABM,
∵四边形ABED是圆内接四边形,
∴∠ADE+∠ABE=180°,
又∠ADE+∠MDE=180°,
∴∠MDE=∠MBA,
同理证明:∠MED=∠A,
∴∠MDE=∠MED,
∴MD=ME.
(2)①由(1)可知,∠A=∠MDE,
∴DE∥AB,
∴$\frac{DE}{AB}$=$\frac{MD}{MA}$,
∵AD=2DM,
∴DM:MA=1:3,
∴DE=$\frac{1}{3}$AB=$\frac{1}{3}$×6=2.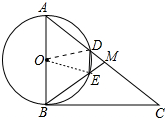
故答案为2.
②当∠A=60°时,四边形ODME是菱形.
理由:连接OD、OE,
∵OA=OD,∠A=60°,
∴△AOD是等边三角形,
∴∠AOD=60°,
∵DE∥AB,
∴∠ODE=∠AOD=60°,∠MDE=∠MED=∠A=60°,
∴△ODE,△DEM都是等边三角形,
∴OD=OE=EM=DM,
∴四边形OEMD是菱形.
故答案为60°.
点评 本题考查圆内接四边形性质、直角三角形斜边中线性质、菱形的判定等知识,解题的关键是灵活运用这些知识解决问题,记住菱形的三种判定方法,属于中考常考题型.


科目:初中数学 来源: 题型:选择题
| A. | 2:1 | B. | 7:5 | C. | 17:12 | D. | 24:17 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
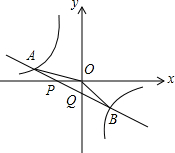 如图,已知直线y=k1x+b与x轴、y轴相交于P、Q两点,与y=$\frac{{k}_{2}}{x}$的图象相交于A(-2,m)、B(1,n)两点,连接OA、OB,给出下列结论:①k1k2<0;②m+$\frac{1}{2}$n=0;③S△AOP=S△BOQ;④不等式k1x+b$>\frac{{k}_{2}}{x}$的解集是x<-2或0<x<1,其中正确的结论的序号是②③④.
如图,已知直线y=k1x+b与x轴、y轴相交于P、Q两点,与y=$\frac{{k}_{2}}{x}$的图象相交于A(-2,m)、B(1,n)两点,连接OA、OB,给出下列结论:①k1k2<0;②m+$\frac{1}{2}$n=0;③S△AOP=S△BOQ;④不等式k1x+b$>\frac{{k}_{2}}{x}$的解集是x<-2或0<x<1,其中正确的结论的序号是②③④.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x1=4,x2=-4 | B. | x1=2,x2=-2 | C. | x1=x2=0 | D. | x1=2$\sqrt{3}$,x2=-2$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com