练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，在△ABC中，∠B=70°，AB=4，BC=6，将△ABC沿图示中的虚线DE剪开，剪下的三角形与原三角形相似的有（ ）

    (1) (2) (3) (4)

    A. 1个 B. 2个 C. 3个 D. 4个

    C 【解析】 图1，∵∠CDE=∠B=70°, ∠C=∠C, ∴△CDE∽△CBA； 图2，∵∠CED=∠B=70°, ∠C=∠C, ∴△CDE∽△CAB； 图3，∵AC的长度不知道，∴无法说明 ,∴△ADE与△ABC不一定相似； 图4，∵∠BDE=∠A=70°, ∠BED=∠C, ∴△BDE∽△BAC； 故选C.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：湖南省武冈市2017-2018学年八年级上学期期末考试数学试卷 题型：解答题

    为了创建全国卫生城市，某社区要清理一个卫生死角内的垃圾，租用甲、乙两车运送，两车各运12趟可完成，需支付运费4 800元．已知甲、乙两车单独运完此垃圾，乙车所运趟数是甲车的2倍，且乙车每趟运费比甲车少200元．

    (1)求甲、乙两车单独运完此堆垃圾各需运多少趟？

    (2)若单独租用一台车，租用哪台车合算？

    （1）甲车单独运完此堆垃圾需18趟，乙车需36趟．（2）单独租用乙车合算． 【解析】试题分析：（1）假设甲车单独运完此堆垃圾需运x趟，则乙车单独运完此堆垃圾需运2x趟，根据工作总量=工作时间×工作效率建立方程求出其 解即可； （2）分别表示出甲、乙两车单独运每一趟所需费用，再根据关键语句“两车各运12趟可完成，需支付运费4800元”可得方程，再 解出方程，再分别计算出利用甲或乙所需费用...

    查看答案和解析>>

    科目：初中数学 来源：江西省萍乡市2017-2018学年七年级上学期期末考试数学试卷 题型：单选题

    已知线段AB=10cm，点C是直线AB上一点，BC=4cm，若M是AC的中点，N是BC的中点，则线段MN的长度是（　　）

    A. 7cm B. 3cm C. 7cm或3cm D. 5cm

    D 【解析】（1）当点C在线段AB上时，则MN=AC+BC=AB=5； （2）当点C在线段AB的延长线上时，则MN=AC-BC=7-2=5． 综合上述情况，线段MN的长度是5cm． 故选D．

    查看答案和解析>>

    科目：初中数学 来源：江苏省泰兴市2018届九年级上学期期末考试数学试卷 题型：解答题

    先化简，再求值： ，其中a=－2．

    【解析】试题分析：本题考查了分式的化简求值，先把除法转化为乘法，并把分子、分母分解因式约分化简，再计算分式的加减，最后代入求值即可. = = =. 当a=－2时， 原式=.

    查看答案和解析>>

    科目：初中数学 来源：江苏省泰兴市2018届九年级上学期期末考试数学试卷 题型：填空题

    已知一组数据1，3，5，7，则该组数据的方差S2=_________.

    5 【解析】, ∴.

    查看答案和解析>>

    科目：初中数学 来源：江苏省泰兴市2018届九年级上学期期末考试数学试卷 题型：单选题

    －2018的倒数是（ ）

    A. 2018 B. C. D. －2018

    B 【解析】∵乘积为1的两个数互为倒数， ∴－2018的倒数是. 故选B.

    查看答案和解析>>

    科目：初中数学 来源：甘肃省天水市2017-2018学年七年级上学期期末模四考试数学试卷 题型：解答题

    解方程：

    （1）4x-3（5-x）=6 （2）

    （1）3；（2）-0.4 ． 【解析】试题分析：（1）按去括号、移项、合并同类项、系数化为1的步骤进行求解即可； （2）按去分母、去括号、移项、合并同类项、系数化为1的步骤进行求解即可. 试题解析：（1）4x-15+3x=6， 4x+3x=6+15， 7x=21， x=3； （2）4（2x-1）=3（x+2）-12， 8x-4=3x+6-12， ...

    查看答案和解析>>

    科目：初中数学 来源：甘肃省天水市2017-2018学年七年级上学期期末模四考试数学试卷 题型：单选题

    如图，点P是线段AB上的点，其中不能说明点P是线段AB中点的是（ ）

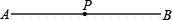
    A. AB＝2AP B. AP＝BP C. AP＋BP＝AB D.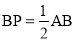

    C 【解析】试题分析：根据线段中点的定义，对选项进行一一分析，排除错误答案． 【解析】 A、若AB=2AP，则P是线段AB中点； B、若AP=BP，则P是线段AB中点； C、AP+BP=AB，P可是线段AB是任意一点； D、若BP=AB，则P是线段AB中点． 故选：C．

    查看答案和解析>>

    科目：初中数学 来源：北京市延庆区2017-2018学年第一学期八年级期末数学试卷 题型：解答题

    如图，点A、F、C、D在同一条直线上．AB∥DE，∠B=∠E，AF=DC．求证：BC=EF．

    答案见解析 【解析】先利用AAS证明△ABC≌△DEF，再根据全等三角形的性质即可得出结论． 证明：∵AB∥DE， ∴∠A=∠D． ∵AF=DC， ∴AF+FC=DC+FC ∴AC=DF． 在△ABC和△DEF中， ∴△ABC≌△DEF（AAS）， ∴BC=EF．

    查看答案和解析>>

    同步练习册答案