
【题目】如图,在平面直角坐标系中,抛物线行![]() 经过点
经过点![]() 和点
和点![]() ,交
,交![]() 轴正半轴于点
轴正半轴于点![]() ,连接
,连接![]() ,点
,点![]() 是线段
是线段![]() 上动点(不与点
上动点(不与点![]() 重合),以
重合),以![]() 为边在
为边在![]() 轴上方作正方形
轴上方作正方形![]() ,接
,接![]() ,将线段
,将线段![]() 绕点
绕点![]() 逆时针旋转90°,得到线段
逆时针旋转90°,得到线段![]() ,过点
,过点![]() 作
作![]() 轴,
轴,![]() 交抛物线于点
交抛物线于点![]() ,设点
,设点![]() .
.
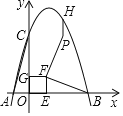
(1)求抛物线的解析式;
(2)若![]() 与
与![]() 相似求
相似求![]() 的值;
的值;
(3)当![]() 时,求点
时,求点![]() 的坐标.
的坐标.
【答案】(1)y=-x2+3x+4;(2)a=![]() 或
或![]() ;(3)点P的坐标为(1,4)或(2,4)或(
;(3)点P的坐标为(1,4)或(2,4)或(![]() ,4)
,4)
【解析】
(1)点C(0,4),则c=4,二次函数表达式为:y=-x2+bx+4,将点A的坐标代入上式,即可求解;
(2)△AOC与△FEB相似,则∠FBE=∠ACO或∠CAO,即:tan∠FEB=![]() 或4,即可求解;
或4,即可求解;
(3)证明△PNF≌△BEF(AAS),PH=2,则-4a2+6a+4-4=|2|,即可求解.
解:(1)将点A和点C的坐标代入上式得:0=-1-b+4,
解得:b=3,
故抛物线的表达式为:y=-x2+3x+4;
(2)∵tan∠ACO=![]() =
=![]() ,
,
△AOC与△FEB相似,则∠FBE=∠ACO或∠CAO,
∴tan∠FBE=![]() 或4,
或4,
∵四边形OEFG为正方形,则FE=OE=a,EB=4-a,
则![]() 或
或![]() ,
,
解得:a=![]() 或
或![]() ;
;
(3)令y=-x2+3x+4=0,解得:x=4或-1,故点B(4,0);
分别延长GF、HP交于点N,
∵∠PFN+∠BFN=90°,∠FPN+∠PFN=90°,
∴∠FPN=∠NFB,
∵GN∥x轴,∴∠FPN=∠NFB=∠FBE,
∵∠PNF=∠BEF=90°,FP=FB,
∴△PNF≌△BEF(AAS),
∴FN=FE=a,PN=EB=4-a,
∴点P(2a,4),点H(2a,-4a2+6a+4),
∵PH=2,
即:-4a2+6a+4-4=±2,
解得:a=1或![]() 或
或![]() 或
或![]() (舍去),
(舍去),
故:点P的坐标为(1,4)或(2,4)或(![]() ,4).
,4).



 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:
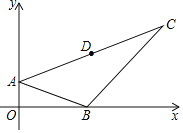
【题目】如图,点A、B分别在y轴和x轴正半轴上滑动,且保持线段AB=4,点D坐标为(4,3),点A关于点D的对称点为点C,连接BC,则BC的最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场甲、乙、丙三名业务员2018年前5个月的销售额(单位:万元)如下表:
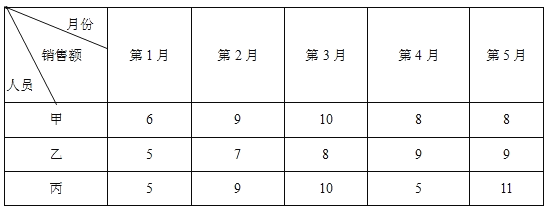
(1)根据上表中的数据,将下表补充完整:
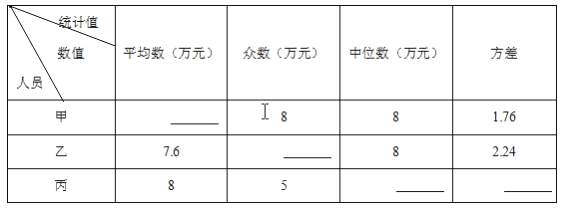
(2)甲、乙、丙三名业务员都说自己的销售业绩好,你赞同谁的说法?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
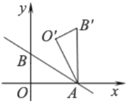
【题目】如图,直线![]() 与
与![]() 轴、y轴分别交于A、B两点,把△AOB绕点A顺时针旋转60°后得到△AO′B′,则点B'的坐标是( )
轴、y轴分别交于A、B两点,把△AOB绕点A顺时针旋转60°后得到△AO′B′,则点B'的坐标是( )
A. (4, ![]() ) B. (
) B. (![]() ,4) C. (
,4) C. (![]() ,3) D. (
,3) D. (![]() ,
, ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为6的正方形![]() 中,
中,![]() 分别是
分别是![]() 上的点,
上的点,![]() ,
,![]() 为垂足.
为垂足.
(1)如图①, AF=BF,AE=2![]() ,点T是射线PF上的一个动点,则当△ABT为直角三角形时,求AT的长;
,点T是射线PF上的一个动点,则当△ABT为直角三角形时,求AT的长;
(2)如图②,若![]() ,连接
,连接![]() ,求证:
,求证:![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】己知:如图1,⊙O的半径为2, BC是⊙O的弦,点A是⊙O上的一动点。

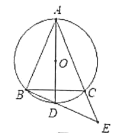
图1 图2
(1)当△ABC的面积最大时,请用尺规作图确定点A位置(尺规作图只保留作图痕迹, 不需要写作法);
(2)如图2,在满足(1)条件下,连接AO并延长交⊙O于点D,连接BD并延长交AC 的延长线于点E,若∠BAC=45° ,求AC2+CE2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校艺术节计划为学生购买A、B两种奖品,已知购买40件A种奖品和购买60件B种奖品共需2600元,购买35件A种奖品和购买70件B种奖品共需2800元.
(1)求A、B两种奖品的单价各为多少元?
(2)若学校购买A、B两种奖品共100件,且购买这批奖品的总费用不超过2800元,求最多购买B奖品多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
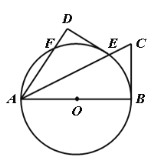
【题目】如图,已知AB是⊙O的直径,F是⊙O上一点,∠BAF的平分线交⊙O于点E,交⊙O的切线BC于点C,过点E作ED⊥AF,交AF的延长线于点D.
(1)求证:DE是⊙O的切线;
(2)若DE=3,CE=2,
①求![]() 值;
值;
②若点G 为AE上一点,求OG+![]() EG最小值.
EG最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一张矩形纸片,长15cm,宽9cm,在它的四角各剪去一个同样的小正方形,然折叠成一个无盖的长方体纸盒.若纸盒的底面(图中阴影部分)面积是48cm2,求剪去的小正方形的边长.设剪去的小正方形边长是xcm,根据题意可列方程为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com