
分析 (1)根据销售利润=销售量w×(销售价单x-成本单价),列出函数关系式;
(2)根据销售利润y=(每千克销售价-每千克进价)×销售量w,列函数关系式,用配方法将(2)的函数关系式变形,利用二次函数的性质求最大值;
(3)把y=150代入(2)的函数关系式中,解一元二次方程求x,根据x的取值范围求x的值
解答 解:(1)y=w(x-20)=(x-20)(-2x+80)=-2x2+120x-1600;
(2)y=(x-20)(-2x+80)=-2x2+80x+40x-1600=-2x2+120x-1600=-2(x-30)2+200,
∵a=-2<0,
∴抛物线开口向下,且当x=30时,y最大=200;
(3)当y=150时,150=-2(x-30)2+200,
(x-30)2=25,
x-30=±5,
x=30±5,
x1=25,x2=35(舍去)
又∵y=-2x2+120x-1600=-2(x-30)2+200,
∴当x=28时,能取得最大值为192.
答:农户每天能获得比150元更大的利润,最大利润是192元.
点评 本题考查了二次函数的运用.关键是根据题意列出函数关系式,运用二次函数的性质解决问题.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:初中数学 来源: 题型:解答题
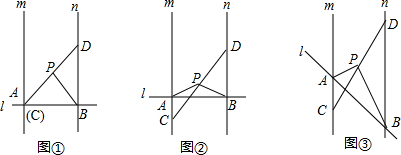
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:一个正比例函数和一个一次函数的图象交于点P(-2、2)且一次函数的图象与y轴的 交点Q的纵坐标为4.
已知:一个正比例函数和一个一次函数的图象交于点P(-2、2)且一次函数的图象与y轴的 交点Q的纵坐标为4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com