【题目】解下列方程或方程组
（1）2x﹣1＝x+9
（2）x+5＝2（x﹣1）
（3）
（4）
【答案】（1）
（2）
（3）
（4）
【解析】
解：（1）对移项合并2x﹣1＝x+9即可得到答案；
（2）先去括号得x+5＝2x﹣2，移项合并，再系数化为1即可得到答案；
（3）去分母得20﹣5x＝3x﹣9﹣15，移项合并，再系数化为1即可得到答案；
（4）去分母得40﹣15x+35＝﹣4x﹣68，移项合并，再系数化为1即可得到答案．
解：（1）对2x﹣1＝x+9移项合并得：x＝10；
（2）去括号得：x+5＝2x﹣2，
移项合并得：﹣x＝﹣7，
系数化为1得：x＝7；
（3）去分母得：20﹣5x＝3x﹣9﹣15，
移项合并得：﹣8x＝﹣44，
系数化为1得：x＝5.5；
（4）去分母得：40﹣15x+35＝﹣4x﹣68，
移项合并得：﹣11x＝﹣143，
系数化为1得：x＝13．
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】如图A在数轴上对应的数为-2.
(1)点B在点A右边距离A点4个单位长度，则点B所对应的数是_____.
(2)在(1)的条件下，点A以每秒2个单位长度沿数轴向左运动，点B以每秒3个单位长度沿数轴向右运动.现两点同时运动,当点A运动到-6的点处时，求A、B两点间的距离.
(3)在(2)的条件下，现A点静止不动，B点以原速沿数轴向左运动，经过多长时间A、B两点相距4个单位长度.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某餐厅中，一张桌子可坐6人，有以下两种摆放方式：
（1）有4张桌子，用第一种摆设方式，可以坐 人；用第二种摆设方式，可以坐 人；
（2）有n张桌子，用第一种摆设方式可以坐 人；用第二种摆设方式，可以坐 人（用含有n的代数式表示）；
（3）一天中午，餐厅要接待120位顾客共同就餐，但餐厅中只有30张这样的长方形桌子可用，且每6张拼成一张大桌子，若你是这家餐厅的经理，你打算选择哪种方式来摆放餐桌，为什么？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，∠C=90°，AD平分∠CAB，交CB于点D，过点D作DE⊥AB，于点E
（1）求证：△ACD≌△AED；
（2）若∠B=30°，CD=1，求BD的长。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读下面的材料：
符号、p分别表示一种运算，它对一些数的运算结果如下：
（0）=-1， （1）=0 ， （2）=1 ， （-3）=-4， （-4）=-5，……
p（-1）=-2，p（
）=1，p（
）=
， p（2）=4， p（-3）=-6，……
根据以上运算规律，完成下列问题：
（1）计算：（-5）×p（
）+2
（2）已知x为有理数，且（x）+ p（
）=2×（-4），求x的值。
查看答案和解析>>
科目：初中数学 来源： 题型：
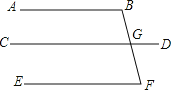
【题目】如图：已知∠B＝∠BGD，∠DGF＝∠F，求证：∠B+∠F＝180°．
请你认真完成下面的填空．
证明：∵∠B＝∠BGD （ 已知 ）
∴AB∥CD （ ）
∵∠DGF＝∠F；（ 已知 ）
∴CD∥EF （ ）
∴AB∥EF （ ）
∴∠B+∠F＝180°（ ）．
查看答案和解析>>
科目：初中数学 来源： 题型：
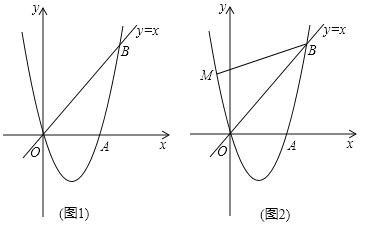
【题目】如图1，经过原点O的抛物线
（a≠0）与x轴交于另一点A（
，0），在第一象限内与直线y=x交于点B（2，t）．
（1）求这条抛物线的表达式；
（2）在第四象限内的抛物线上有一点C，满足以B，O，C为顶点的三角形的面积为2，求点C的坐标；
（3）如图2，若点M在这条抛物线上，且∠MBO=∠ABO，在（2）的条件下，是否存在点P，使得△POC∽△MOB？若存在，求出点P的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】观察下列两个等式：
，
，给出定义如下：我们称使等式
成立的一对有理数“
，
”为“共生有理数对”，记为（，）．
(1)通过计算判断数对“2,1,“4,
”是不是“共生有理数对”；
(2)若(6,a)是“共生有理数对”，求a的值；
(3)若(m,n)是“共生有理数对”,则“n,m”___“共生有理数对”(填“是”或“不是”)，并说明理由；
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，方格纸中每个小方格都是边长为1个单位长度的正方形，在建立平面直角坐标系后，△ABC的顶点坐标为A（1，-4），B（5，-4），C（4，-1）．
（1）在方格纸中画出△ABC；
（2）求出△ABC的面积；
（3）若把△ABC向上平移6个单位长度，再向左平移7个单位长度得到△A′B′C′，在图中画出△A′B′C′，并写出B′的坐标．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com