
分析 利用平方差公式、完全平方公式、提公因式法进行因式分解即可.
解答 解:(1)(1-a2)(1-b2)-(a2-1)2(b2-1)2;
=(1-a2)(1-b2)[1-(1-a2)(1-b2)]
=(a+1)(a-1)(b+1)(b-1)(a2+b2-a2b2);
(2)(x+1)2-9(x-1)2
=(x+1)2-[3(x-1)]2
=(x+1+3x-3)(x+1-3x+3)
=4(2x-1)(2-x);
(3)4a2b2-(a2+b2-c2)2
=(2ab)2-(a2+b2-c2)2
=(2ab-a2-b2+c2)(2ab+a2+b2-c2)
=[c2-(a-b)2][-c2+(a+b)2]
=(c+a-b)(c-a+b)(a+b+c)(a+b-c);
(4)ab2-ac2+4ac-4a
=a(b2-c2+4c-4)
=a[b2-(c-2)2]
=a(b+c-2)(b-c+2).
点评 本题考查的是多项式的因式分解,掌握提公因式法、公式法、分组分解法是解题的关键.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
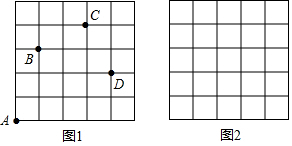
 如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动.它从A处出发去看望B、C、D处的其他甲虫.规定:向上、向右走为正,向下、向左走为负.如从A到B记为:A→B(+1,+4),从B到A记为:A→B(-1,-4),括号内第一个数表示左右方向,第二个数表示上下方向,那么图中
如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动.它从A处出发去看望B、C、D处的其他甲虫.规定:向上、向右走为正,向下、向左走为负.如从A到B记为:A→B(+1,+4),从B到A记为:A→B(-1,-4),括号内第一个数表示左右方向,第二个数表示上下方向,那么图中查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
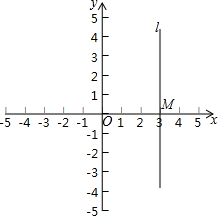 如图,在平面直角坐标系中,直线l过点M(3,0),且平行于y轴.
如图,在平面直角坐标系中,直线l过点M(3,0),且平行于y轴.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com