
【题目】在平面直角坐标系中,点![]() 为坐标原点,直线
为坐标原点,直线![]() 过点
过点![]() 且与
且与![]() 轴平行,直线
轴平行,直线![]() 过点
过点![]() 且与
且与![]() 轴平行,直线
轴平行,直线![]() 与
与![]() 相交于
相交于![]() .点
.点![]() 为直线
为直线![]() 上一点,反比例函数
上一点,反比例函数![]() 的图象过点
的图象过点![]() 且与直线
且与直线![]() 相交于点
相交于点![]() .
.
(1)若点![]() 与点
与点![]() 重合,求
重合,求![]() 的值;
的值;
(2)连接![]() 、
、![]() 、
、![]() ,若
,若![]() 的面积为
的面积为![]() 面积的2倍,求点
面积的2倍,求点![]() 的坐标;
的坐标;
(3)当![]() 时,在
时,在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使
,使![]() 是等腰直角三角形?如果存在,直接写出
是等腰直角三角形?如果存在,直接写出![]() 点坐标:若不存在,说明理由.
点坐标:若不存在,说明理由.
【答案】(1)2;(2)点E的坐标为(![]() ,2)或(3,2)时
,2)或(3,2)时![]() 的面积为
的面积为![]() 面积的2倍;(3)当
面积的2倍;(3)当![]() 时,G(0,1)或(0,
时,G(0,1)或(0, ![]() ),此时
),此时![]() 是等腰直角三角形
是等腰直角三角形
【解析】
(1)根据平行线的性质得到点P的坐标,由点E与点P重合得到点E的坐标,将点E的坐标代入![]() 中即可求出k的值;
中即可求出k的值;
(2)根据题意画出图形,用k表示点E及点F的坐标,得到对应线段的长度,分三种情况利用![]() 的面积为
的面积为![]() 面积的2倍分别求出k的值,即可得到点E的坐标;
面积的2倍分别求出k的值,即可得到点E的坐标;
(3)由![]() 知点E在点P的右边,点F在点P的上边,画出图象,设点E的坐标及点F的坐标,分三种情况,根据等腰直角三角形的性质证明全等即可求出答案.
知点E在点P的右边,点F在点P的上边,画出图象,设点E的坐标及点F的坐标,分三种情况,根据等腰直角三角形的性质证明全等即可求出答案.
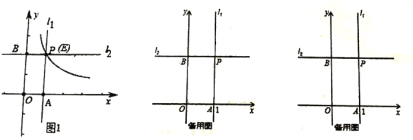
(1)由题意得点P(1,2),
∵点![]() 与点
与点![]() 重合,
重合,
∴E(1,2),
∵![]() 的图象过点
的图象过点![]() ,
,
∴k=![]() ;
;
(2)①当0<k<2时,如图1,
根据题意知:四边形OAPB是矩形,BP=1,AP=2,,
∵点E、F都在反比例函数![]() 的图象上,
的图象上,
∴E(![]() ,2),F(1,k),
,2),F(1,k),
∴BE=![]() ,PE=1-
,PE=1-![]() ,AF=k,PF=2-k,
,AF=k,PF=2-k,
∵![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
∴![]() ,
,
解得![]() ,
, ![]() (舍去),
(舍去),
∴E(![]() ,2);
,2);
当k=2时,△OEF不存在;
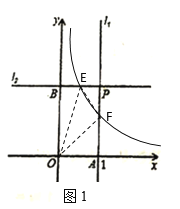
②当k>2时,如图2,过点E作x轴的垂线EC,垂足为C,过点F作y轴的垂线FD,垂足为D,EC和FD相交于点H,则四边形OCHD是矩形,
∵E(![]() ,2),F(1,k),
,2),F(1,k),
∴PE=![]() -1,PF=k-2,
-1,PF=k-2,
∴![]() ,
,
∵四边形PEGF是矩形,
∴![]()
∵![]() ,
,
![]() ,
,
=![]() ,
,
∴![]() =2
=2![]() ,
,
解得![]() ,
,![]() (舍去),
(舍去),
∴E(3,2),
综上,点E的坐标为(![]() ,2)或(3,2)时
,2)或(3,2)时![]() 的面积为
的面积为![]() 面积的2倍;
面积的2倍;
(3)存在,
∵k>0,
∴点E在点P的右边,点F在点P的上边,
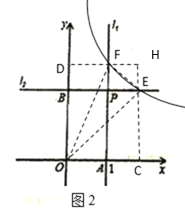
①如图3,∠FEG=90°,EF=EG,
设E(m,2),则F(1,2m),
∵∠EPF=EBG,EF=EG,∠FEP=∠BGE,
∴△FEP≌△EGB,
∴PF=BE,BG=EP,
∴m=2m-2,
∴m=2,
∴BG=PE=1,
∴G(0,1);

②如图4,∠EFG=90°,EF=FG,作FM⊥y轴,
设E(m,2),则F(1,2m),
可得△FEP≌△FMG,
∴FM=FP,MG=EP,
∴2m-2=1,
∴m=![]() ,
,
∴F(1,3),E(![]() ,2),
,2),
∴MG=PE=![]() -1=
-1=![]() ,
,
∴G(0, ![]() );
);

③∠EGF=90°的情况不存在,
综上,当![]() 时,G(0,1)或(0,
时,G(0,1)或(0, ![]() ),此时
),此时![]() 是等腰直角三角形.
是等腰直角三角形.


科目:初中数学 来源: 题型:
【题目】定义:在平面直角坐标系中,O为坐标原点,设点P的坐标为(x,y),当x<0时,点P的变换点P′的坐标为(﹣x,y);当x≥0时,点P的变换点P′的坐标为(﹣y,x).
(1)若点A(2,1)的变换点A′在反比例函数y=![]() 的图象上,则k= ;
的图象上,则k= ;
(2)若点B(2,4)和它的变换点B'在直线y=ax+b上,则这条直线对应的函数关系式为 ,∠BOB′的大小是 度.
(3)点P在抛物线y=x2﹣2x﹣3的图象上,以线段PP′为对角线作正方形PMP'N,设点P的横坐标为m,当正方形PMP′N的对角线垂直于x轴时,求m的取值范围.
(4)抛物线y=(x﹣2)2+n与x轴交于点C,D(点C在点D的左侧),顶点为E,点P在该抛物线上.若点P的变换点P′在抛物线的对称轴上,且四边形ECP′D是菱形,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
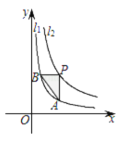
【题目】如图,函数![]() (x>0)和
(x>0)和![]() (x>0)的图象分别是
(x>0)的图象分别是![]() 和
和![]() .设点P在
.设点P在![]() 上,PA∥y轴交
上,PA∥y轴交![]() 于点A,PB∥x轴,交
于点A,PB∥x轴,交![]() 于点B,△PAB的面积为( )
于点B,△PAB的面积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在眉山市樱花节期间,岷江二桥一端的空地上有一块矩形的标语牌ABCD(如图).已知标语牌的高AB=5m,在地面的点E处,测得标语牌点A的仰角为30°,在地面的点F处,测得标语牌点A的仰角为75°,且点E,F,B,C在同一直线上,求点E与点F之间的距离.(计算结果精确到0.1m,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列一元二次方程中,两实根之和为1的是 ( )
A. x2—x+1=0 B. x2+x—3=0 C. 2 x2-x-1=0 D. x2-x-5=0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,E,F分别在边AC、BC上,满足AE=CF,连接BE,AF交于点P.
(1)求证:△ABE≌△CAF;
(2)求∠APB的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点![]() ,经过A、B的直线
,经过A、B的直线![]() 以每秒1个单位的
以每秒1个单位的
速度向下作匀速平移运动,与此同时,点P从点B出发,在直线![]() 上以每秒1个单位的速度沿直线
上以每秒1个单位的速度沿直线![]() 向右下方向作匀速运动.设它们运动的时间为
向右下方向作匀速运动.设它们运动的时间为![]() 秒.
秒.

(1)用含![]() 的代数式表示点P的坐标;
的代数式表示点P的坐标;
(2)过O作OC⊥AB于C,过C作CD⊥![]() 轴于D,问:
轴于D,问: ![]() 为何值时,以P为圆心、1为半径的圆与直线OC相切?并说明此时
为何值时,以P为圆心、1为半径的圆与直线OC相切?并说明此时![]() 与直线CD的位置关系.
与直线CD的位置关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,实数与数轴上的点是一一对应的,任意一个实数在数轴上都能找到与之对应的点,比如我们可以在数轴上找到与数字2对应的点.
(1)在如图所示的数轴上,画出一个你喜欢的无理数,并用点![]() 表示;
表示;
(2)(1)中所取点![]() 表示的数字是______,相反数是_____,绝对值是______,倒数是_____,其到点5的距离是______.
表示的数字是______,相反数是_____,绝对值是______,倒数是_____,其到点5的距离是______.
(3)取原点为![]() ,表示数字1的点为
,表示数字1的点为![]() ,将(1)中点
,将(1)中点![]() 向左平移2个单位长度,再取其关于点
向左平移2个单位长度,再取其关于点![]() 的对称点
的对称点![]() ,求
,求![]() 的长.
的长.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小敏的爸爸买了某项体育比赛的一张门票,她和哥哥两人都很想去观看.可门票只有一张,读九年级的哥哥想了一个办法,拿了8张扑克牌,将数字为2,3,5,9的四张牌给小敏,将数字为4,6,7,8的四张牌留给自己,并按如下游戏规则进行:小敏和哥哥从各自的四张牌中随机抽出一张,然后将两人抽出的两张扑克牌数字相加,如果和为偶数,则小敏去;如果和为奇数,则哥哥去.
【1】请用画树形图或列表的方法求小敏去看比赛的概率;
【2】哥哥设计的游戏规则公平吗?若公平,请说明理由;若不公平,请你设计一种公平的游戏规则.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com