
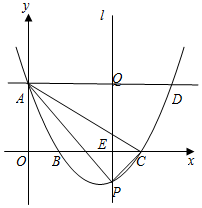
 如图,在平面直角坐标系中,抛物线y=mx2-8mx+4m+2(m>0)与y轴交于点A(0,3),与x轴交于点B、C(B在C的左边),直线AD∥x轴交抛物线于点D,x轴上有一动点E(t,0),过点E作平行于y轴的直线l与抛物线、AD分别交于P、Q.
如图,在平面直角坐标系中,抛物线y=mx2-8mx+4m+2(m>0)与y轴交于点A(0,3),与x轴交于点B、C(B在C的左边),直线AD∥x轴交抛物线于点D,x轴上有一动点E(t,0),过点E作平行于y轴的直线l与抛物线、AD分别交于P、Q.分析 (1)把点A(0,3)代入y=mx2-8mx+4m+2,求出m即可,令y=0,得到x2-8x+12=0,解得x=2或6,可得B(2,0)、C(6,0);
(2)分两种情形①当0<t<6时,②当6≤t≤8时,分别求解即可解决问题;
(3)分两种情况讨论:①当2<t<8时,AQ=t,PQ=$-\frac{1}{4}{t^2}+2t$若△AOB∽△AQP,若△AOB∽△PQA,分别列出方程求解;
②当t>8时,AQ=t,PQ=$\frac{1}{4}{t^2}-2t$若△AOB∽△AQP,若△AOB∽△PQA,分别列出方程求解即可;
解答 解:(1)把点A(0,3)代入y=mx2-8mx+4m+2,得3=4m+2,
∴m=$\frac{1}{4}$,
∴该抛物线解析式为:y=$\frac{1}{4}{x^2}-2x+3$;
令y=0,得到x2-8x+12=0,解得x=2或6,
∴B(2,0)、C(6,0).
(2)设直线AC的解析式为:y=kx+b,
∴$\left\{\begin{array}{l}6k+b=0\\ b=3\end{array}\right.$
解得$\left\{\begin{array}{l}k=-\frac{1}{2}\\ b=3\end{array}\right.$
∴直线AC的解析式为:y=-$\frac{1}{2}$x+3,
设△APC面积为S,
要构成△APC,显然t≠6,
分两种情况讨论:
设直线l与AC交点为F,
∴P(t,$\frac{1}{4}{t^2}-2t+3$)
F(t,$-\frac{1}{2}t+3$),
①当0<t<6时,
PF=$-\frac{1}{4}{t^2}+\frac{3}{2}t$,
∴S=$\frac{1}{2}(-\frac{1}{4}{t^2}+\frac{3}{2}t)×6$
=$-\frac{3}{4}{({t-3})^2}+\frac{27}{4}$,
此时S最大值为:$\frac{27}{4}$.
②当6≤t≤8时,
PF=$\frac{1}{4}{t^2}-\frac{3}{2}t$,
∴S=$\frac{1}{2}({\frac{1}{4}{t^2}-\frac{3}{2}t})×6$
=$\frac{3}{4}{({t-3})^2}-\frac{27}{4}$
∵当t>3时,s随t的增大而增大,
∴当t=8时,S取最大值为:12.
综上可知,当0<t≤8时,
△APC面积的最大值为12.
(3)连接AB,则△AOB中,
∠AOB=90°,AO=3,BO=2,
Q(t,3),P(t,$\frac{1}{4}{t^2}-2t+3$),
要构成△APQ,显然t≠8,
分两种情况讨论:
①当2<t<8时,
AQ=t,PQ=$-\frac{1}{4}{t^2}+2t$
若△AOB∽△AQP,
则AO:AQ=OB:QP,
即3:t=2:($-\frac{1}{4}{t^2}+2t$),
∴t=0(舍),或t=$\frac{16}{3}$,
若△AOB∽△PQA,
则AO:PQ=OB:QA,
即2:t=3:($-\frac{1}{4}{t^2}+2t$),
∴t=0(舍)或t=2(舍),
②当t>8时,
AQ=t,PQ=$\frac{1}{4}{t^2}-2t$
若△AOB∽△AQP,
则AO:AQ=OB:QP,
即3:t=2:($\frac{1}{4}{t^2}-2t$),
∴t=0(舍),或t=$\frac{32}{3}$,
若△AOB∽△PQA,
则AO:PQ=OB:QA,
即2:t=3:($\frac{1}{4}{t^2}-2t$),
∴t=0(舍)或t=14,
综上所述,满足条件的t的值为t$\frac{16}{3}$s或$\frac{32}{3}$s或14s.
点评 本题考查二次函数综合题、一次函数的应用、相似三角形的判定和性质、三角形的面积问题等知识,解题的关键是学会构建二次函数解决最值问题,学会用分类讨论的思想思考问题,学会用方程的思想思考问题,属于中考压轴题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
 尺规作图
尺规作图查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x$>\frac{1}{3}$ | B. | x≥$\frac{1}{3}$ | C. | x≥-$\frac{1}{3}$ | D. | x>-$\frac{1}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
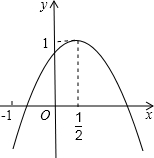 如图,二次函数y=ax2+bx+c的图象与y轴正半轴相交,其顶点坐标为(0.5,1),下列结论:
如图,二次函数y=ax2+bx+c的图象与y轴正半轴相交,其顶点坐标为(0.5,1),下列结论:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
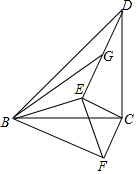 如图,在等腰直角△BCD中,∠BCD=90°,BC=CD,E为△BCD内一点,且CE⊥DE,DE=2CE,将△CDE绕点C逆时针旋转90°得到△CBF,连接EF、BE,G为DE的中点,连接BG.如果△BDG的面积为1cm2,那么BG的长度为$\sqrt{10}$cm.
如图,在等腰直角△BCD中,∠BCD=90°,BC=CD,E为△BCD内一点,且CE⊥DE,DE=2CE,将△CDE绕点C逆时针旋转90°得到△CBF,连接EF、BE,G为DE的中点,连接BG.如果△BDG的面积为1cm2,那么BG的长度为$\sqrt{10}$cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com