
【题目】如图,在矩形A′B′CD中,A′B′=10, B′C=8,以CD为直径作⊙O.将矩形A′B′CD绕点C旋转,使所得矩形ABCD′的边AB与⊙O相切,切点为E.
(1)证明:CE平分∠BCD;
(2)求线段AE的长.
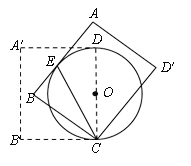
【答案】(1)详见解析;(2)6
【解析】
(1)连接OE,利用切线的性质证得OE⊥AB,根据矩形的性质和旋转的性质得到∠B=90°,即可证得OE∥BC,利用平行线的性质即可得到结论;
(2)过点O作OF⊥BC于点F,得到四边形OEBF为矩形,求出OE得到CF,即可根据勾股定理求出OF,由此得到答案.
(1)连接OE,
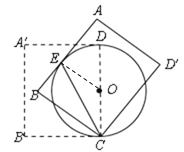
∵直线AB与⊙O的相切,
∴OE⊥AB,
在矩形A′B′CD中∠B′=90°,
由旋转可知∠B=90°,
∴OE∥BC,
∴∠BCE=∠OEC,
∴OE=OC,
∴∠OCE=∠OEC,
∴∠OCE=∠BCE,
即CE平分∠BCD;
(2)过点O作OF⊥BC于点F,
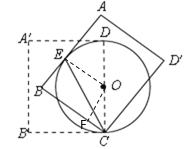
则四边形OEBF为矩形,
∴BF=OE=10÷2=5,
∴CF=8-5=3,
Rt△OFC中,![]() ,
,
∴AE=AB-BE=AB-OF=10-4=6.


 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:
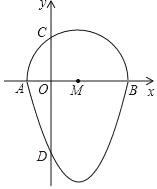
【题目】如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”.已知点A、B、C、D分别是“果圆”与坐标轴的交点,抛物线的解析式为y=x2﹣6x﹣16,AB为半圆的直径,则这个“果圆”被y轴截得的线段CD的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
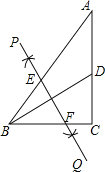
【题目】如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,点D是AC的中点,连接BD,按以下步骤作图:①分别以B,D为圆心,大于![]() BD的长为半径作弧,两弧相交于点P和点Q;②作直线PQ交AB于点E,交BC于点F,则BF=( )
BD的长为半径作弧,两弧相交于点P和点Q;②作直线PQ交AB于点E,交BC于点F,则BF=( )
A. ![]() B. 1C.
B. 1C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从如图所示的二次函数![]() (
(![]() )的图象中,观察得出了下面5条信息:①
)的图象中,观察得出了下面5条信息:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() .你认为其中正确的信息有( )
.你认为其中正确的信息有( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
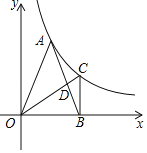
【题目】如图,A为反比例函数y=![]() (其中x>0)图象上的一点,在x轴正半轴上有一点B,OB=4.连接OA、AB,且OA=AB=2
(其中x>0)图象上的一点,在x轴正半轴上有一点B,OB=4.连接OA、AB,且OA=AB=2![]() .
.
(1)求k的值;
(2)过点B作BC⊥OB,交反比例函数y=![]() (x>0)的图象于点C.
(x>0)的图象于点C.
①连接AC,求△ABC的面积;
②在图上连接OC交AB于点D,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
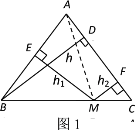
【题目】(阅读)如图1,在等腰△ABC中,AB=AC,AC边上的高为h,M是底边BC上的任意一点,点M到腰AB、AC的距离分别为h1,h2.连接AM.
∵![]() ∴
∴![]()
(思考)在上述问题中,h1,h2与h的数量关系为: .
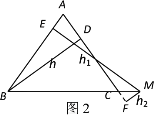
(探究)如图2,当点M在BC延长线上时,h1、h2、h之间有怎样的数量关系式?并说明理由.
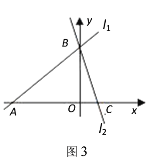
(应用)如图3,在平面直角坐标系中有两条直线l1:![]() ,l2:y=-3x+3,若l2上的一点M到l1的距离是1,请运用上述结论求出点M的坐标.
,l2:y=-3x+3,若l2上的一点M到l1的距离是1,请运用上述结论求出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读以下材料,并按要求完成相应地任务:
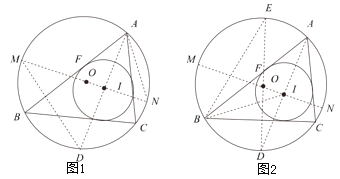
莱昂哈德·欧拉(Leonhard Euler)是瑞士数学家,在数学上经常见到以他的名字命名的重要常数,公式和定理,下面是欧拉发现的一个定理:在△ABC中,R和r分别为外接圆和内切圆的半径,O和I分别为其外心和内心,则![]() .下面是该定理的证明过程(部分):
.下面是该定理的证明过程(部分):
延长AI交⊙O于点D,过点I作⊙O的直径MN,连接DM,AN.
∵∠D=∠N,∴∠DMI=∠NAI(同弧所对的圆周角相等),
∴△MDI∽△ANI.∴![]() ,∴
,∴![]() ①
①
如图2,在图1(隐去MD,AN)的基础上作⊙O的直径DE,连接BE,BD,BI,IF
∵DE是⊙O的直径,∴∠DBE=90°.
∵⊙I与AB相切于点F,∴∠AFI=90°,
∴∠DBE=∠IFA.
∵∠BAD=∠E(同弧所对圆周角相等),
∴△AIF∽△EDB.
∴![]() ,∴
,∴![]() ②
②

任务:(1)观察发现:![]() ,
,![]() (用含R,d的代数式表示);
(用含R,d的代数式表示);
(2)请判断BD和ID的数量关系,并说明理由.
(3)请观察式子①和式子②,并利用任务(1),(2)的结论,按照上面的证明思路,完成该定理证明的剩余部分;
(4)应用:若△ABC的外接圆的半径为5cm,内切圆的半径为2cm,则△ABC的外心与内心之间的距离为 cm.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com