
【题目】如图①,在矩形ABCD中,动点P从A点出发沿折线AD﹣DC﹣CB运动,当点P运动到点B时停止.已知动点P在AD、BC上的运动速度为1cm/s,在DC上的运动速度为2cm/s.△PAB的面积y(cm2)与动点P的运动时间t(s)的函数关系图象如图②.


(1)a=______,b=______;
(2)用文字说明点N坐标的实际意义;
(3)当t为何值时,y的值为2cm2.
【答案】 4, 6;
(2)P运动了4s时到达点C,此时△PAB的面积为4cm2;
(3)t为1s或5s时,y的值为2cm2.
【解析】试题分析:(1)从图②中根据面积和运动时间求出AD,AB,从而得到a、b;(2)从图②中点N的纵坐标和横坐标分别考虑,结合图①即可;(3)y是2cm2的话,因为AB=4,只有点P到AB的距离为1,此时求得t值即可.
试题解析:
(1)由图②中发现,点P从开始运动到2s时运动到点D,且在AD边上速度为1,
∴BC=AD=2,∵点P在DC上运动时,面积不变是4,∴4=0.5AB×AD,∴AB=4,
∵DC上的运动速度为2cm/s,∴a=2+4÷2=4,∴b=2+2+2=6,故答案为4,6;
(2)P运动了4s时到达点C,此时△PAB的面积为4cm2,
(3)由题意AB=DC=4,∵要y的值为2cm2,即点P到AB的距离为1,
∴必须点P在AD或BC上,且PA=1cm或PB=1cm,
当PA=1cm时,点P的运动时间t=1s,
当PB=1cm时,点P的运动时间为t=6﹣1=5s,
即当t为1s或5s时,y的值为2cm2.


科目:初中数学 来源: 题型:
【题目】如图1,有两个全等的直角三角形△ABC和△EDF,∠ACB=∠F=90°,∠A=∠E=30°,点D在边AB上,且AD=BD=CD.△EDF绕着点D旋转,边DE,DF分别交边AC于点M,K.
(1)如图2、图3,当∠CDF=0°或60°时,AM+CKMK(填“>”,“<”或“=”),你的依据是;

(2)如图4,当∠CDF=30°时,AM+CKMK(填“>”或“<”);
(3)猜想:如图1,当0°<∠CDF<60°时,AM+CKMK,试证明你的猜想..
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠A=60°,∠ABC,∠ACB所对的边b,c满足:b ![]() +c
+c ![]() -4(b+c)+8=0.
-4(b+c)+8=0.
(1)证明:△ABC是边长为2的等边三角形.
(2)若 b,c两边上的中线BD,CE交于点O,求OD:OB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(﹣1,2),且与X轴交点的横坐标分别为x1,x2,其中﹣2<x1<﹣1,0<x2<1,下列结论:①4a﹣2b+c<0;②2a﹣b<0;③a+c<1;④b2+8a>4ac.其中正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,顶点为P(4,-4)的二次函数图象经过原点(0,0),点A在该图象上,OA交其对称轴l于点M,点M、N关于点P对称,连接AN、ON.
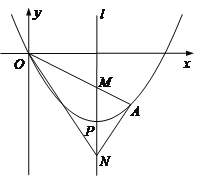
(1)求该二次函数的关系式;
(2)若点A的坐标是(6,-3),求△ANO的面积;
(3)当点A在对称轴l右侧的二次函数图象上运动时,请解答下面问题:
①证明:∠ANM=∠ONM;
②△ANO能否为直角三角形?如果能,请求出所有符合条件的点A的坐标;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】制作一种产品,需先将材料加热达到60℃后,再进行操作.设该材料温度为y(℃),从加热开始计算的时间为x(分钟).据了解,该材料加热时,温度y与时间x成一次函数关系;停止加热进行操作时,温度y与时间x成反比例关系(如图).已知该材料在操作加工前的温度为15℃,加热5分钟后温度达到60℃.

(1)分别求出将材料加热和停止加热进行操作时,y与x的函数关系式;
(2)根据工艺要求,当材料的温度低于15℃时,须停止操作,那么从开始加热到停止操作,共经历了多少时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件为必然事件的是( )
A.小王参加本次数学考试,成绩是150分
B.某射击运动员射靶一次,正中靶心
C.打开电视机,CCTV第一套节目正在播放新闻
D.口袋中装有2个红球和1个白球,从中摸出2个球,其中必有红球
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com