
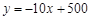 .
.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:不详 题型:解答题
 ,若存在,求出P点坐标;若不存在,请说明理由.
,若存在,求出P点坐标;若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 ,下列说法:①当
,下列说法:①当 时,
时,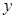 随
随 的增大而减小;②若图象与
的增大而减小;②若图象与 轴有交点,则
轴有交点,则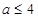 ;③当
;③当 时,不等式
时,不等式 的解集是
的解集是 ;④若将图象向上平移1个单位,再向左平移3个单位后过点
;④若将图象向上平移1个单位,再向左平移3个单位后过点 ,则
,则 .其中正确的有 (填正确答案的序号).
.其中正确的有 (填正确答案的序号).查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ,0),如图所示:抛物线
,0),如图所示:抛物线 经过点B。
经过点B。
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
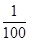 x+150,成本为20元/件,月利润为W内(元);②若只在国外销售,销售价格为150元/件,受各种不确定因素影响,成本为a元/件(a为常数,10≤a≤40),当月销量为x(件)时,每月还需缴纳
x+150,成本为20元/件,月利润为W内(元);②若只在国外销售,销售价格为150元/件,受各种不确定因素影响,成本为a元/件(a为常数,10≤a≤40),当月销量为x(件)时,每月还需缴纳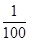 x2元的附加费,月利润为W外(元).
x2元的附加费,月利润为W外(元).查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 图象的一部分,图象过点
图象的一部分,图象过点 (3,0),且对称轴为
(3,0),且对称轴为 ,给出下列四个结论:①
,给出下列四个结论:① ;②
;② ;③
;③ ;④
;④ ,其中正确结论的序号是___________.(把你认为正确的序号都写上)
,其中正确结论的序号是___________.(把你认为正确的序号都写上)
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
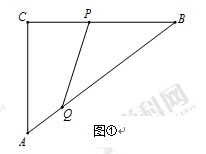
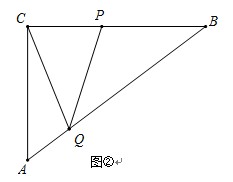
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com