
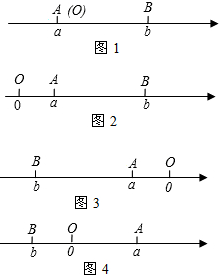
 阅读材料:点A、B在数轴上分别表示实数a、b,A、B两点之间的距离表示为|AB|,当两点中有一点在原点时,不妨设点A在原点.如图1.|AB|=|OB|=|b|=|a-b|;当A,B两点都不在原点时,
阅读材料:点A、B在数轴上分别表示实数a、b,A、B两点之间的距离表示为|AB|,当两点中有一点在原点时,不妨设点A在原点.如图1.|AB|=|OB|=|b|=|a-b|;当A,B两点都不在原点时,分析 ①根据(1)中的知识可以得到两点之间的距离就是较大的数与较小的数的差,据此即可求解;
②根据(1),即可直接写出结果;
③利用-3<x<-2时,当-2≤x<2时,分别求出即可;
④代数式|x-1|+|x+2|表示数轴上一点到1、-2两点的距离的和,根据两点之间线段最短,进而得出答案;
⑤利用y=|x-1|+|x-2|+|x-3|+…+|x-2010|是数轴上点x 与 1、2、3、…2010的距离和,进而得出当1005≤x≤1006 时,y最小求出即可.
解答 解:①数轴上表示-2和-5的两点之间的距离是-2-(-5)=3,
数轴上表示1和-3的两点之间的距离是1-(-3)=4;
故答案为:3;
②数轴上表示x和-1的两点之间的距离是|x+1|,
|AB|=2,则|x+1|=2,故x=1或-3;
故答案为:|x+1|,1或-3;
③当-3<x<-2时,|x+3|+|x+2|=x+3-x-2=1,
当-2≤x<2时,|x+3|+|x+2|=x+3+x+2=2x+5,
故答案为:1或2x+5;
④若|x+1|+|x-2|取最小值,那么表示x的点M在-1和2之间的线段上,
所以-1≤x≤2;
故答案为:-1≤x≤2;
⑤由题意可得:y=|x-1|+|x-2|+|x-3|+…+|x-2010|是数轴上点x 与 1、2、3、…2010的距离和.
所以,当 1005≤x≤1006 时,
y最小=(2010-1)+(2009-2)+(2008-3)+…+(1006-1005)
=2009+2007+2005+…+3+1
=10052
=1010025.
故答案为:1010025.
点评 此题主要考查了绝对值、数轴等知识,用几何方法借助数轴来求解,非常直观,体现了数形结合的优点.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com