
【题目】(11分)如图,四边形ABCD为菱形,点E为对角线AC上的一个动点,连结DE并延长交AB于点F,连结BE.
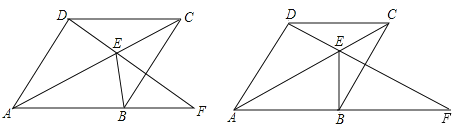
(1)如图①,求证:∠AFD=∠EBC;
(2)如图②,若DE=EC且BE⊥AF,求∠DAB的度数;
(3)若∠DAB=90°且当△BEF为等腰三角形时,求∠EFB的度数(只写出条件与对应的结果)
【答案】(1)证明见试题解析;(2)60°;(3)30°或120°.
【解析】
试题(1)利用“SAS”得出△DCE≌△BCE,即可得出答案;
(2)利用等腰三角形的性质结合垂直的定义得出∠DAB的度数;
(3)分两种情况讨论:①当F在AB延长线上时,②当F在线段AB上时,分别求出即可.
试题解析:(1)∵四边形ABCD为菱形,∴DC=CB,在△DCE和△BCE中,∵DC=CB,∠DCE=∠BCE,EC=EC,∴△DCE≌△BCE(SAS),∴∠EDC=∠EBC,∵DC∥AB,∴∠EDC=∠AFD,∴∠AFD=∠EBC;
(2)∵DE=EC,∴∠EDC=∠ECD,设∠EDC=∠ECD=∠CBE=x°,则∠CBF=2x°,由BE⊥AF得:2x+x=90°,解得:x=30°,∴∠DAB=∠CBF=60°;
(3)分两种情况:①如图1,当F在AB延长线上时,
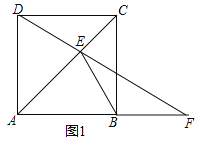
∵∠EBF为钝角,∴只能是BE=BF,设∠BEF=∠BFE=x°,则:90+x+x+x=180,解得:x=30,∴∠EFB=30°;
②如图2,当F在线段AB上时,
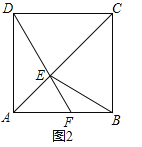
∵∠EFB为钝角,∴只能是FE=FB,设∠BEF=∠EBF=x°,则有∠AFD=2x°,可证得:∠AFD=∠FDC=∠CBE,得x+2x=90,解得:x=30,∴∠EFB=120°,
综上所述:∠EFB=30°或120°.


科目:初中数学 来源: 题型:
【题目】阅读理解题:
定义:如果一个数的平方等于,记为![]() ,这个数
,这个数![]() 叫做虚数单位,把形如
叫做虚数单位,把形如![]() (a,b为实数)的数叫做复数,其中a叫这个复数的实部,b叫做这个复数的虚部.它的加,减,乘法运算与整式的加,减,乘法运算类似.
(a,b为实数)的数叫做复数,其中a叫这个复数的实部,b叫做这个复数的虚部.它的加,减,乘法运算与整式的加,减,乘法运算类似.
例如计算:![]() ;
;
![]()
根据以上信息,完成下列问题:
(1)填空:![]() ,
,![]() ;
;
(2)计算:![]() ;
;
(3)计算:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A,O,B依次在直线MN上,如图1,现将射线OA绕点O顺时针方向以每秒10°的速度旋转,同时射线OB绕着点O按逆时针方向以每秒15°的速度旋转,直线MN保持不动,如图2,设旋转时间为t秒(t≤12).
(1)在旋转过程中,当t=2时,求∠AOB的度数.
(2)在旋转过程中,当∠AOB=105°时,求t的值.
(3)在旋转过程中,当OA或OB是某一个角(小于180°)的角平分线时,求t的值.
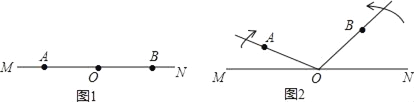
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:矩形ABCD中,AB=4,BC=3,点M、N分别在边AB、CD上,直线MN交矩形对角线 AC于点E,将△AME沿直线MN翻折,点A落在点P处,且点P在射线CB上.
(1)如图1,当EP⊥BC时,求CN的长;
(2) 如图2,当EP⊥AC时,求AM的长;
(3) 请写出线段CP的长的取值范围,及当CP的长最大时MN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABOC的顶点A的坐标为(-4,5),D是OB的中点,E是OC上的一点,当△ADE的周长最小时,点E的坐标是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A,B,C三点在数轴上的位置如图所示,它们表示的数分别是a,b,c.
(1)填空:abc 0,a+b 0,ab﹣ac 0;(填“>”,“=”或“<”)
(2)若|a|=2且点B到点A,C的距离相等,
①当b2=16时,求c的值;
②P是数轴上B,C两点之间的一个动点,设点P表示的数为x,当P点在运动过程中,bx+cx+|x﹣c|﹣10|x+a|的值保持不变,求b的值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某车间有技术工人85人,平均每天每人可加工甲种部件16个或乙种部件10个,2个甲种部件和3个乙种部件配成一套,问加工甲、乙两种部件各安排多少人才能使每天加工的两种部件刚好配套?并求出加工了多少套?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一袋中装有形状大小都相同的四个小球,每个小球上各标有一个数字,分别是1,4,7,8.现规定从袋中任取一个小球,对应的数字作为一个两位数的个位数;然后将小球放回袋中并搅拌均匀,再任取一个小球,对应的数字作为这个两位数的十位数.
(1)写出按上述规定得到所有可能的两位数;
(2)从这些两位数中任取一个,求其算术平方根大于4且小于7的概率.
【答案】(1)16种等可能的结果数,它们是:11,41,71,81,14,44,74,84,17,47,77,87,18,48,78,88;(2)![]()
【解析】(1)画树状图:

共有16种等可能的结果数,它们是:11,41,71,81,14,44,74,84,17,47,77,87,18,48,78,88;
(2)算术平方根大于4且小于7的结果数为6,
所以算术平方根大于4且小于7的概率=![]() =3/8.
=3/8.
【题型】解答题
【结束】
23
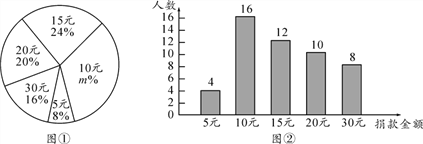
【题目】某高校学生会向全校2900名学生发起了“爱心一日捐”捐款活动,为了解捐款情况,学生会随机调查了部分学生的捐款金额,并用得到的数据绘制了如下统计图①和图②,请根据相关信息,解答下列问题:
(1)本次接受随机抽样调查的学生人数为____,图①中m的值是____;
(2)求本次你调查获取的样本数据的平均数、众数和中位数;
(3)根据样本数据,估计该校本次活动捐款金额为10元的学生人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com