
| A. | 2倍 | B. | 4倍 | C. | 50% | D. | 100% |
分析 扇形面积=$\frac{nπ{r}^{2}}{360}$,若“把一个扇形的圆心角扩大到原来2倍,半径缩小到原来的一半”,则扇形面积变成$\frac{nπ{r}^{2}}{2×360}$,从而可以比较面积大小关系.
解答 解:原扇形面积=$\frac{nπ{r}^{2}}{360}$,
变化后的扇形面积=$\frac{2nπ\frac{{r}^{2}}{4}}{360}$=$\frac{nπ{r}^{2}}{2×360}$,
则变化后的面积是原来面积的$\frac{1}{2}$,即其面积变为原来的50%;
故选:C.
点评 本题考查了扇形面积的计算,解答此题的关键是:利用扇形面积公式,将变化后的面积与原面积比较即可求解.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 方差 | B. | 平均数 | C. | 众数 | D. | 中位数 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
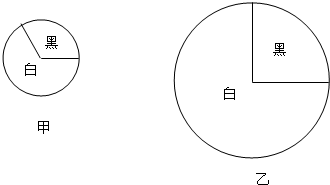 如图,有甲、乙两个圆,它们的半径之比为3:8,每个圆又都被分割成黑、白两个扇形,其中甲圆被分成的黑、白两个扇形的面积之比为1:2,乙圆被分成的黑、白两个扇形的面积之比为1:3,那么图中两个黑色扇形的面积之和与两个白色扇形的面积之和的比是19:54.(直接写出答案)
如图,有甲、乙两个圆,它们的半径之比为3:8,每个圆又都被分割成黑、白两个扇形,其中甲圆被分成的黑、白两个扇形的面积之比为1:2,乙圆被分成的黑、白两个扇形的面积之比为1:3,那么图中两个黑色扇形的面积之和与两个白色扇形的面积之和的比是19:54.(直接写出答案)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com