
 ���������C1�Ķ�����������C2�ϣ�ͬʱ��������C2�Ķ���Ҳ��������C1�ϣ���ô���dz�������C1��C2������
���������C1�Ķ�����������C2�ϣ�ͬʱ��������C2�Ķ���Ҳ��������C1�ϣ���ô���dz�������C1��C2���������� ��1��������������ߢٵĶ������꣬Ȼ������Ƿ�˵��������ߢ�����ϣ�����������ߢڵĶ������꣬�����Ƿ��������ߢ��ϣ�������ô𰸣�
��2���������������C1�Ķ������꣬��ɵã���P��ֱ��y=1�ϣ������M����P�ĶԳƵ�N���ֱ����M��N��ֱ��y=1�Ĵ��ߣ�����ΪE��F�������õ�N�����꣬���ö���ʽ������ý����
��3��������������C1��y=a1��x-m��2+n��C2��y=a2��x-p��2+q����������$\left\{\begin{array}{l}{q={a}_{1}��p-m��^{2}+n��}\\{n={a}_{1}��m-p��^{2}+q��}\end{array}\right.$��+�ڵã�a1+a2����m-p��2=0���������a1+a2=0��
��� 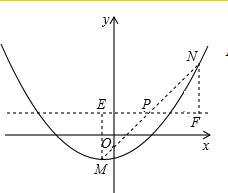 �⣺��1���ߢ�������y=x2+2x-7=��x+1��2-8�Ķ�������ΪM��-1��-8����
�⣺��1���ߢ�������y=x2+2x-7=��x+1��2-8�Ķ�������ΪM��-1��-8����
��ڵ�x=-1ʱ��y=-x2+4x-3=-1-4-3=-8��
���M�������ߢ��ϣ�
�������ߢ��������ߢ��й�����
�������ߢ�y=-x2+4x-3=-��x-2��2+1���䶥������Ϊ��2��1����
�����㣺��2��1���������ߢ��ϣ�
�������ߢ١����ǹ����ģ�
��2��������C1��y=$\frac{1}{6}$��x+1��2-2�Ķ���M������Ϊ��-1��-2����
�߶���P������Ϊ��t��1����
���P��ֱ��y=1�ϣ�
��M����P�ĶԳƵ�N���ֱ����M��N��ֱ��y=1�Ĵ��ߣ�����ΪE��F����ME=NF=3��
���N��������Ϊ4��
��y=3ʱ��$\frac{1}{6}$��x+1��2-2=4��
��ã�x1=5��x2=-7��
��������C2�Ľ���ʽΪ��y=a��x-5��2+4��
�ߵ�M��-1��-2����������C2�ϣ�
��-2=a��-1-5��2+4��
��a=-$\frac{1}{6}$��
��������C2�Ľ���ʽΪ��y=-$\frac{1}{6}$��x-5��2+4��
��������C2�Ľ���ʽΪ��y=a��x+7��2+4��
�ߵ�M��-1��-2����������C2�ϣ�
��-2=a��-1+7��2+4��
��a=-$\frac{1}{6}$��
��������C2�Ľ���ʽΪ��y=-$\frac{1}{6}$��x+7��2+4��
��3��Сӱͬѧ�IJ�����ȷ��
���ɣ��߶��㲻ͬ������������C1��y=a1��x-m��2+n��C2��y=a2��x-p��2+q������
����$\left\{\begin{array}{l}{q={a}_{1}��p-m��^{2}+n}\\{n={a}_{2}��m-p��^{2}+q}\end{array}\right.$
��+�ڵã�a1+a2����m-p��2=0��
��m��p��
��a1+a2=0��
�����ʽ�еĶ�����ϵ��һ���ǻ�Ϊ�෴����
���� ���⿼���˴���ϵ��������κ����Ľ���ʽ�Լ����κ����Ķ����������ⷽ����ȫ�������ε����ʵ�֪ʶ�������ۺ��Ժ�ǿ���ѶȽϴ�ע�����ν��˼�����������˼���Ӧ�ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1.2��105 | B�� | 1.2��106 | C�� | 1.2��107 | D�� | 1.2��108 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ʵ��a��b��c�������ϵ�λ����ͼ��ʾ�������ʽ|a+b|-|b-a|+|a-c|+c=��������
ʵ��a��b��c�������ϵ�λ����ͼ��ʾ�������ʽ|a+b|-|b-a|+|a-c|+c=��������| A�� | -3a+2c | B�� | -a-ab-2c | C�� | a-2b | D�� | 3a |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
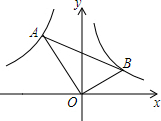 ��ͼ��Rt��AOB�У���AOB=90�㣬��A��˫����y=$\frac{k}{x}$��x��0���ϣ���B��˫����y=$\frac{1}{x}$��x��0���ϣ�
��ͼ��Rt��AOB�У���AOB=90�㣬��A��˫����y=$\frac{k}{x}$��x��0���ϣ���B��˫����y=$\frac{1}{x}$��x��0���ϣ��鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com