
 (2012•乐山)如图,在东西方向的海岸线l上有一长为1千米的码头MN,在码头西端M的正西方向30 千米处有一观察站O.某时刻测得一艘匀速直线航行的轮船位于O的北偏西30°方向,且与O相距20
(2012•乐山)如图,在东西方向的海岸线l上有一长为1千米的码头MN,在码头西端M的正西方向30 千米处有一观察站O.某时刻测得一艘匀速直线航行的轮船位于O的北偏西30°方向,且与O相距20| 3 |
| 2 |
| 3 |
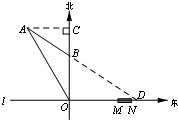 解(1)过点A作AC⊥OB于点C.由题意,得
解(1)过点A作AC⊥OB于点C.由题意,得| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
| ||
| 2 |
| AC2+BC2 |
(10
|
| 40 |
| 60 |
| 3 |
| 3 |


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
 (2012•乐山)如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,有下列结论:
(2012•乐山)如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,有下列结论:| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
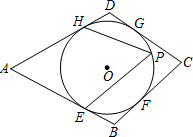 (2012•乐山)如图,⊙O是四边形ABCD的内切圆,E、F、G、H是切点,点P是优弧
(2012•乐山)如图,⊙O是四边形ABCD的内切圆,E、F、G、H是切点,点P是优弧 | EFH |
查看答案和解析>>
科目:初中数学 来源: 题型:
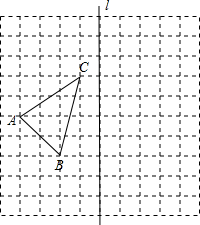 (2012•乐山)如图,在10×10的正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).
(2012•乐山)如图,在10×10的正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com