
【题目】在平面直角坐标系中,点A,B的坐标分别为(1,0),(3,0),现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD.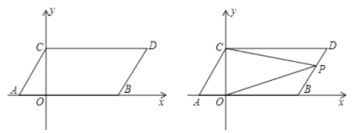
(1)求点C,D的坐标及四边形ABDC的面积S四边形ABDC;
(2)在y轴上是否存在一点P,连接PA,PB,使S△PAB=S四边形ABDC?若存在这样一点,求出点P的坐标;若不存在,试说明理由;
(3)点P是直线BD上一个动点,连接PC、PO,当点P在直线BD上运动时,请直接写出∠OPC与∠PCD、∠POB的数量关系.
【答案】(1) C(0,2),D(4,2),S四边形ABDC=8.
(2)存在.证明见解析.
(3) ①∠OPC=∠PCD+∠POB;
②∠OPC=∠POB∠PCD;
③∠OPC=∠PCD∠POB.
【解析】
(1)根据C、D两点在坐标系中的位置即可得出此两点坐标;判断出四边形ABDC是平行四边形,再求出其面积即可;
(2)设点P到AB的距离为h,则S△PAB=![]() ×AB×h=2h,由S△PAB=S四边形ABDC,得2h=8,求出h=4,即可得出点P的坐标;
×AB×h=2h,由S△PAB=S四边形ABDC,得2h=8,求出h=4,即可得出点P的坐标;
(3)过点P作PQ∥AB,故可得出CD∥PQ,AB∥PQ,由平形线的性质即可得出结论.
(1)依题意,得C(0,2),D(4,2),四边形ABDC是平行四边形,
∴S四边形ABDC=AB×OC=4×2=8;
(2)存在.理由如下:
设点P到AB的距离为h,则S△PAB=![]() ×AB×h=2h,
×AB×h=2h,
∵S△PAB=S四边形ABDC,
∴2h=8,
解得:h=4,
∴P(0,4)或(0,4);
(3)过点P作PQ∥AB,交y轴于点Q,
∵四边形ABDC是平行四边形,
∴CD∥PQ,
①点P在线段BD上,如图1所示: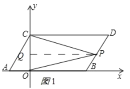
∵CD∥PQ,AB∥PQ,
∴∠CPQ=∠PCD,∠OPQ=∠POB,
∴∠OPC=∠CPQ+∠OPQ=∠PCD+∠POB
②点P在BD延长线上,且在CD的上方时,
如图2所示: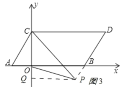
∵CD∥PQ,AB∥PQ,
∴∠CPQ=∠PCD,∠OPQ=∠POB,
∴∠OPC=∠OPQ∠CPQ=∠POB∠PCD;
③点P在DB延长线上,且在AB的下方时,
如图3所示: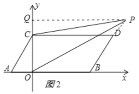
∵CD∥PQ,AB∥PQ,
∴∠CPQ=∠PCD,∠OPQ=∠POB,
∴∠OPC=∠CPQ∠OPQ=∠PCD∠POB.


科目:初中数学 来源: 题型:
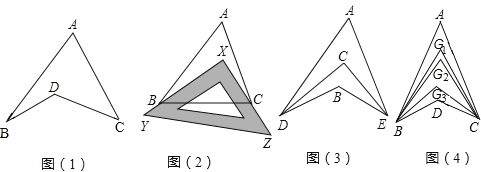
【题目】探究与发现:如图1所示的图形,像我们常见的学习用品﹣﹣圆规.我们不妨把这样图形叫做“规形图”.
(1)观察“规形图”,试探究∠BDC与∠A、∠B、∠C之间的关系,并说明理由;
(2)请你直接利用以上结论,解决以下三个问题:
①如图2,把一块三角尺XYZ放置在△ABC上,使三角尺的两条直角边XY、XZ恰好经过点B、C,∠A=40°,则∠ABX+∠ACX= °;
②如图3,DC平分∠ADB,EC平分∠AEB,若∠DAE=40°,∠DBE=130°,求∠DCE的度数;
③如图4,∠ABD,∠ACD的10等分线相交于点G1、G2…、G9,若∠BDC=133°,∠BG1C=70°,求∠A的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小李购买了一套一居室,他准备将房子的地面铺上地砖,地面结构如图所示,根据图中所给的数据![]() 单位:米
单位:米![]() ,解答下列问题:
,解答下列问题:
![]() 用含m,n的代数式表示地面的总面积S;
用含m,n的代数式表示地面的总面积S;
![]() 已知客厅面积是卫生间面积的8倍,且卫生间、卧室、厨房面积的和比客厅还少3平方米,如果铺1平方米地砖的平均费用为100元,那么小李铺地砖的总费用为多少元?
已知客厅面积是卫生间面积的8倍,且卫生间、卧室、厨房面积的和比客厅还少3平方米,如果铺1平方米地砖的平均费用为100元,那么小李铺地砖的总费用为多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
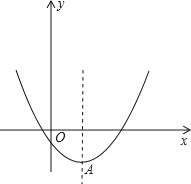
【题目】已知二次函数y=x2﹣2mx+4m﹣8,
(1)当x≤2时,函数值y随x的增大而减小,求m的取值范围.
(2)以抛物线y=x2﹣2mx+4m﹣8的顶点A为一个顶点作该抛物线的内接正三角形AMN(M,N两点在拋物线上),请问:△AMN的面积是与m无关的定值吗?若是,请求出这个定值;若不是,请说明理由.
(3)若抛物线y=x2﹣2mx+4m﹣8与x轴交点的横坐标均为整数,求整数m的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
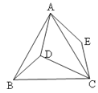
【题目】如图,在等边△ABC内有一点D,AD=4,BD=3,CD=5,将△ABD绕A点逆时针旋转,使AB与AC重合,点D旋转至点E,则四边形ADCE的面积为( )
A.12B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算题
(1)(3ab)2(﹣![]() ab3)
ab3)
(2)20182﹣2016×2020(利用乘法公式计算)
(3)﹣12019+(﹣![]() )﹣2+
)﹣2+![]() ﹣(π﹣3.14)0
﹣(π﹣3.14)0
(4)[2(x+2y)2﹣(x+y)(4x﹣y)﹣9y2]÷(﹣2x),其中x=﹣2,y=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=12,AC=BC=10,将△ABC绕点A按顺时针方向旋转,得到△ADE,旋转角为α(0°<α<180°),点B的对应点为D,点C的对应点为E,连接BD,BE.
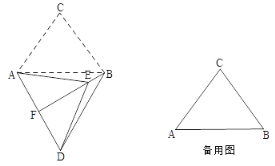
(1)如图,当α=60°时,延长BE交AD于点F.
①求证:△ABD是等边三角形;
②求证:BF⊥AD,AF=DF;
③请直接写出BE的长.
(2)在旋转过程中,过点D作DG垂直于直线AB,垂足为G,连接CE,当∠DAG=∠ACB,且线段DG与线段AE无公共点时,请直接写出BE+CE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在直角坐标平面内,抛物线y=x2+bx+c经过点A(2,0)、B(0,6).
(1)求抛物线的表达式;
(2)抛物线向下平移几个单位后经过点(4,0)?请通过计算说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料,请回答下列问题.
材料一:我国古代数学家秦九韶在《数书九章》中记述了“三斜求积术”,即已知三角形的三边长,求它的面积,用现代式子表示即为: ①(其中
①(其中![]() 为三角形的三边长,
为三角形的三边长,![]() 为面积),而另一个文明古国古希腊也有求三角形面积的“海伦公式”;
为面积),而另一个文明古国古希腊也有求三角形面积的“海伦公式”;![]() ……②(其中
……②(其中![]() )
)
材料二:对于平方差公式:![]() 公式逆用可得:
公式逆用可得:![]() ,例:
,例:![]()
(1)若已知三角形的三边长分别为4,5,7,请分别运用公式①和公式②,计算该三角形的面积;
(2)你能否由公式①推导出公式②?请试试,写出推导过程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com