
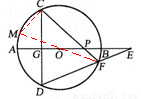
已知:AB是⊙O的直径,弦CD⊥AB于点G,E是直线AB上一动点(不与点A、B、G重合),直线DE交⊙O于点F,直线CF交直线AB于点P.设⊙O的半径为r.
(1)如图1,当点E在直径AB上时,试证明:OE•OP=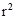 ;
;
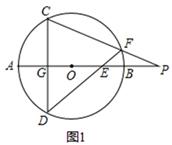
(2)当点E在AB(或BA)的延长线上时,以如图2点E的位置为例,请你画出符合题意的图形,标注上字母,(1)中的结论是否成立?请说明理由.
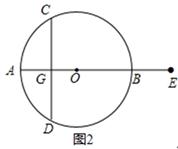
(1)证明见解析;(2)成立, 理由见解析.
【解析】
试题分析:(1)要证等积式,需要将其化为比例式,再利用相似证明. 观察图形,此题显然要连半径OF,构造OE、OP所在的三角形, 这样问题便转化为证明△FOE∽△POF. 而要证明△FOE∽△POF,由于已经存在一个公共角,因此只需再证明另一角对应相等即可,这一点利用圆周角定理及其推论可获证.(2)同(1)类似.
试题解析:(1)连接FO并延长交⊙O于Q,连接DQ.
∵FQ是⊙O直径,∴∠FDQ=90°. ∴∠QFD+∠Q=90°.
∵CD⊥AB,∴∠P+∠C=90°.
∵∠Q=∠C,∴∠QFD=∠P.
∵∠FOE=∠POF,∴△FOE∽△POF. ∴ . ∴OE·OP=OF2=r2.
. ∴OE·OP=OF2=r2.
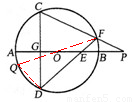
(2)当点E在AB(或BA)的延长线上时,(1)中的结论成立. 理由如下:
依题意画出图形(如图),连接FO并延长交⊙O于M,连接CM.
∵FM是⊙O直径,∴∠FCM=90°. ∴∠M+∠CFM=90°.
∵CD⊥AB,∴∠E+∠D=90°.
∵∠M=∠D,∴∠CFM=∠E.
∵∠POF=∠FOE,∴△POF∽△FOE. ∴ . ∴OE·OP=OF2=r2.
. ∴OE·OP=OF2=r2.
考点:1.圆周角定理;2.相似三角形的判定和性质;3.三角形内角和定理.


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•钦州)如图,某大楼的顶部树有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1:
(2013•钦州)如图,某大楼的顶部树有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1:| 3 |
| 3 |
| 2 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在平面直角坐标系中,直y=
如图,在平面直角坐标系中,直y=| 3 |
| 2 |
| 16 |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
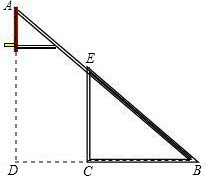
 红星中学篮球课外活动小组的同学自己动手制作一副简易篮球架.如图,是篮球架的侧面示意图,已知篮板所在直线AD和直杆EC都与BC垂直,BC=2.8米,CD=1.8米,∠ABD=40°,求斜杆AB与直杆EC的长分别是多少米?(计算结果精确到0.01米,参考数据:(sin40°≈0.588,cos40°≈0.809,tan40°≈0.727.)
红星中学篮球课外活动小组的同学自己动手制作一副简易篮球架.如图,是篮球架的侧面示意图,已知篮板所在直线AD和直杆EC都与BC垂直,BC=2.8米,CD=1.8米,∠ABD=40°,求斜杆AB与直杆EC的长分别是多少米?(计算结果精确到0.01米,参考数据:(sin40°≈0.588,cos40°≈0.809,tan40°≈0.727.)查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com