
在6张完全相同的卡片上分别画上线段、等边三角形、平行四边形、直角梯形、双曲线、圆,在看不见图形的情况下随机摸出1张,这张卡片上的图形既是中心对称图形又是轴对称图形的概率是( )
A.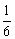 B.
B.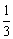 C.
C.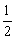 D.
D.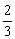
科目:初中数学 来源: 题型:
如果一条抛物线 与
与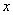 轴有两个交点,那么以该抛物线的顶点和这两个交点为顶 点的三角形称为这条抛物线的“抛物线三角形”.
轴有两个交点,那么以该抛物线的顶点和这两个交点为顶 点的三角形称为这条抛物线的“抛物线三角形”.
(1)“抛物线三角形”一定是 三角形;
(2)若抛物线 的“抛物线三角形”是直角三角形,求
的“抛物线三角形”是直角三角形,求 的值;
的值;
(3)若抛物线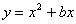 与x轴交与原点O和点B,抛物线的顶点坐标为A,△
与x轴交与原点O和点B,抛物线的顶点坐标为A,△ 是的“抛物线三角形”,是否存在以原点
是的“抛物线三角形”,是否存在以原点 为对称中心的矩形
为对称中心的矩形 ?若存在,求出过
?若存在,求出过 三点的抛物线的表达式;若不存在,说明理由.
三点的抛物线的表达式;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
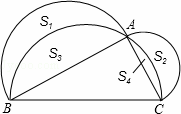
在△ABC中,∠C为锐角,分别以AB,AC为直径作半圆,过点B,A,C作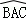 ,如图所示.若AB=4,AC=2,S1﹣S2=
,如图所示.若AB=4,AC=2,S1﹣S2=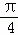 ,则S3﹣S4的值是 (改编)
,则S3﹣S4的值是 (改编)
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,两个同心圆的圆心是O,大圆的半径为10,小圆的半径为6,AD是大圆的直径.大圆的弦AB,BE分别与小圆相切于点C,F.AD,BE相交于点G,连接BD.
(1)求BD 的长;
(2)求∠ABE+2∠D的度数;
(3)求 的值.(改编)
的值.(改编)

查看答案和解析>>
科目:初中数学 来源: 题型:
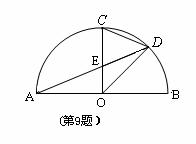
如图,AB是半圆直径,半径OC⊥AB于点O,点D是弧BC的中点,连结CD、AD、OD,给出以下四个结论:①∠DOB=∠ADC;②CE=OE;③△ODE∽△ADO;④2CD2=CE·AB.其中正确结论的序号是( )
A.①③ B.②④ C.①④ D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,抛物线y= x2﹣
x2﹣ x与x轴交于O,A两点.半径为1的动圆(⊙P),圆心从O点出发沿抛物线向靠近点A的方向移动;半径为2的动圆(⊙Q),圆心从A点出发沿抛物线向靠近点O的方向移动.两圆同时出发,且移动速度相等,当运动到P,Q两点重合时同时停止运动.设点P的横坐标为t.若⊙P与⊙Q相离,则t的取值范围是_____ ____ .(根据2013金华模拟改编)
x与x轴交于O,A两点.半径为1的动圆(⊙P),圆心从O点出发沿抛物线向靠近点A的方向移动;半径为2的动圆(⊙Q),圆心从A点出发沿抛物线向靠近点O的方向移动.两圆同时出发,且移动速度相等,当运动到P,Q两点重合时同时停止运动.设点P的横坐标为t.若⊙P与⊙Q相离,则t的取值范围是_____ ____ .(根据2013金华模拟改编)

查看答案和解析>>
科目:初中数学 来源: 题型:
关于二次函数 ,以下结论:① 抛物线交
,以下结论:① 抛物线交 轴有两个不同的交点;②不论k取何值,抛物线总是经过一个定点;③设抛物线交
轴有两个不同的交点;②不论k取何值,抛物线总是经过一个定点;③设抛物线交 轴于A、B两点,若AB=1,则k=9;;④ 抛物线的顶点在
轴于A、B两点,若AB=1,则k=9;;④ 抛物线的顶点在 图像上.其中正确的序号是( )
图像上.其中正确的序号是( )
A.①②③④ B.②③ C.②④ D.①②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com