
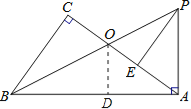
【题目】如图,在Rt△ABC中,∠C=90°,Rt△BAP中,∠BAP=90°,已知∠CBO=∠ABP,BP交AC于点O,E为AC上一点,且AE=OC.
(1)求证:AP=AO;
(2)求证:PE⊥AO;
(3)当AE=![]() AC,AB=10时,求线段BO的长度.
AC,AB=10时,求线段BO的长度.

【答案】(1)证明见解析;
(2)证明见解析;
(3)BO=![]() .
.
【解析】
试题(1)根据等角的余角相等证明即可;
(2)过点O作OD⊥AB于D,根据角平分线上的点到角的两边的距离相等可得CO=DO,利用“SAS”证明△APE和△OAD全等,根据全等三角形对应角相等可得∠AEP=∠ADO=90°,从而得证;
(3)设C0=3k,AC=8k,表示出AE=CO=3k,AO=AP=5k,然后利用勾股定理列式求出PE=4k,BC=BD=10﹣4k,再根据相似三角形对应边成比例列式求出k=1然后在Rt△BDO中,利用勾股定理列式求解即可.
试题解析:(1)∵∠C=90°,∠BAP=90°
∴∠CBO+∠BOC=90°,∠ABP+∠APB=90°,
又∵∠CBO=∠ABP,
∴∠BOC=∠ABP,
∵∠BOC=∠AOP,
∴∠AOP=∠ABP,
∴AP=AO;
(2)如图,过点O作OD⊥AB于D,
∵∠CBO=∠ABP,
∴CO=DO,
∵AE=OC,
∴AE=OD,
∵∠AOD+∠OAD=90°,∠PAE+∠OAD=90°,
∴∠AOD=∠PAE,
在△AOD和△PAE中,
∵AE=OD,∠AOD=∠PAE,AP=AO,
∴△AOD≌△PAE(SAS),
∴∠AEP=∠ADO=90°
∴PE⊥AO;
(3)设AE=OC=3k,
∵AE=![]() AC,∴AC=8k,
AC,∴AC=8k,
∴OE=AC﹣AE﹣OC=2k,
∴OA=OE+AE=5k.
由(1)可知,AP=AO=5k.
如图,过点O作OD⊥AB于点D,
∵∠CBO=∠ABP,∴OD=OC=3k.
在Rt△AOD中,AD=![]() =
=![]() =4k.
=4k.
∴BD=AB﹣AD=10﹣4k.
∵OD∥AP,
∴![]() ,即
,即
![]() ,
,
∵AB=10,PE=AD,
∴PE=AD=4K,BD=AB﹣AD=10﹣4k,
由∠CBO=∠ABP,根据轴对称BC=BD=10﹣4k,
∵∠BOC=∠EOP,∠C=∠PEO=90°,
∴△BCO∽△PEO,
∴![]() ,
,
即![]() ,
,
解得k=1.
∴BD=10﹣4k=6,OD=3k=3,
在Rt△BDO中,由勾股定理得:
BO=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,某农场老板准备建造一个矩形羊圈![]() ,他打算让矩形羊圈的一面完全靠着墙
,他打算让矩形羊圈的一面完全靠着墙![]() ,墙
,墙![]() 可利用的长度为
可利用的长度为![]() ,另外三面用长度为
,另外三面用长度为![]() 的篱笆围成(篱笆正好要全部用完,且不考虑接头的部分)
的篱笆围成(篱笆正好要全部用完,且不考虑接头的部分)

![]() 若要使矩形羊圈的面积为
若要使矩形羊圈的面积为![]() ,则垂直于墙的一边长
,则垂直于墙的一边长![]() 为多少米?
为多少米?
![]() 农场老板又想将羊圈
农场老板又想将羊圈![]() 的面积重新建造成面积为
的面积重新建造成面积为![]() ,从而可以养更多的羊,请聪明的你告诉他:他的这个想法能实现吗?为什么?
,从而可以养更多的羊,请聪明的你告诉他:他的这个想法能实现吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,
,![]() ,
,![]() .
.
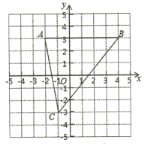
(1)点![]() 到
到![]() 轴的距离为:______;
轴的距离为:______;
(2)![]() 的三边长为:
的三边长为:![]() ______,
______,![]() ______,
______,![]() ______;
______;
(3)当点![]() 在
在![]() 轴上,且
轴上,且![]() 的面积为6时,点
的面积为6时,点![]() 的坐标为:______.
的坐标为:______.
查看答案和解析>>
科目:初中数学 来源: 题型:
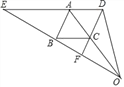
【题目】如图,已知DE∥BC,AO,DF交于点C.∠EAB=∠BCF.
(1)求证:AB∥DF;
(2)求证:OB2=OEOF;
(3)连接OD,若∠OBC=∠ODC,求证:四边形ABCD为菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
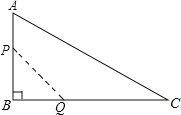
【题目】如图,在△ABC中,∠B=90,∠C=30°,AB=6cm,BC=6![]() cm,动点P从点B开始沿边BA、AC向点C以3cm/s的速度移动,动点Q从点B开始沿边BC向点C以
cm,动点P从点B开始沿边BA、AC向点C以3cm/s的速度移动,动点Q从点B开始沿边BC向点C以![]() cm/s的速度移动,动点P、Q同时出发,到点C运动结束.设运动过程中△BPQ的面积为y(cm2),运动时间为t(s).
cm/s的速度移动,动点P、Q同时出发,到点C运动结束.设运动过程中△BPQ的面积为y(cm2),运动时间为t(s).
(1)点P运动到点A,t= (s);
(2)请你用含t的式子表示y.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班甲、乙、丙三位同学进行了一次用正方形纸片折叠探究相关数学问题的课题学习活动.
活动情境:
如图2,将边长为8cm的正方形纸片ABCD沿EG折叠(折痕EG分别与AB、DC交于点E、G),使点B落在AD边上的点 F处,FN与DC交于点M处,连接BF与EG交于点P.
所得结论:
当点F与AD的中点重合时:(如图1)甲、乙、丙三位同学各得到如下一个正确结论(或结果):
甲:△AEF的边AE=____cm,EF=____cm;
乙:△FDM的周长为16 cm;
丙:EG=BF.
你的任务:
【1】填充甲同学所得结果中的数据;
【2】写出在乙同学所得结果的求解过程;
【3】当点F在AD边上除点A、D外的任何一处(如图2)时:
① 试问乙同学的结果是否发生变化?请证明你的结论;
② 丙同学的结论还成立吗?若不成立,请说明理由,若你认为成立,先证明EG=BF,再求出S(S为四边形AEGD的面积)与x(AF=x)的函数关系式,并问当x为何值时,S最大?最大值是多少?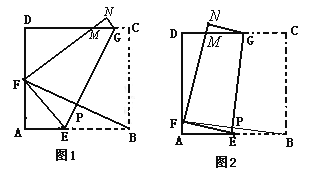
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数![]() 的图像为直线
的图像为直线![]() .
.
(1)若直线![]() 与正比例函数
与正比例函数![]() 的图像平行,且过点(0,2),求直线
的图像平行,且过点(0,2),求直线![]() 的函数表达式;
的函数表达式;
(2)若直线![]() 过点(3,0),且与两坐标轴围成的三角形面积等于3,求
过点(3,0),且与两坐标轴围成的三角形面积等于3,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】位于南岸区黄桷垭的文峰塔,有着“平安宝塔”之称.某校数学社团对其高度 AB进行了测量.如图,他们从塔底A的点B出发,沿水平方向行走了13米,到达点C,然后沿斜坡CD继续前进到达点D处,已知DC=BC.在点D处用测角仪测得塔顶A的仰角为42°(点A,B,C,D,E在同一平面内).其中测角仪及其支架DE高度约为0.5米,斜坡CD的坡度(或坡比)i=1:2.4,那么文峰塔的高度AB约为( )(sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)

A. 22.5 米 B. 24.0 米 C. 28.0 米 D. 33.3 米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将等腰△ABC沿对称轴折叠后,得到△ADC(△ADB),若![]() ,则称等腰△ABC为“长月三角形”ABC.
,则称等腰△ABC为“长月三角形”ABC.

(1)结合题目情境,请你判断“长月三角形”一定会是______三角形.
(2)如图2,C为线段AB上一点,分别以AC和BC为边作“长月三角形”ACD和“长月三角形”BCE,连接AE、BD交于点O,AE与CD交于点P,CE与BD交于点M.
①求证:![]() ;
;
②求![]() 的度数.
的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com