
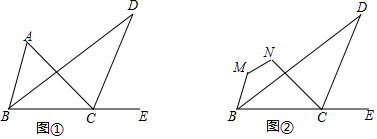
分析 (1)根据三角形内角和定理以及角平分线性质,先求出∠D、∠A的等式,推出∠A=2∠D,最后代入求出即可;
(2)根据(1)中的结论即可得到结论.
解答 解:∵∠ACE=∠A+∠ABC,
∴∠ACD+∠ECD=∠A+∠ABD+∠DBE,∠DCE=∠D+∠DBC,
又BD平分∠ABC,CD平分∠ACE,
∴∠ABD=∠DBE,∠ACD=∠ECD,
∴∠A=2(∠DCE-∠DBC),∠D=∠DCE-∠DBC,
∴∠A=2∠D,
∵∠ABC=75°,∠ACB=45°,
∴∠A=60°,
∴∠D=30°;
(2)∠D=$\frac{1}{2}$(∠M+∠N-180°);
理由:延长BM、CN交于点A,
则∠A=∠BMN+∠CNM-180°,
由(1)知,∠D=$\frac{1}{2}∠$A,
∴∠D=$\frac{1}{2}$(∠M+∠N-180°).
点评 此题考查三角形内角和定理以及角平分线性质的综合运用,解此题的关键是求出∠A=2∠D.


 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com