
����Ŀ�����壺��һ���ı����ܱ�����һ���Խ��߷ָ���������������Σ��������ı���Ϊ���Ѻ��ı��Ρ���
��1����ͼ1����![]() �������������У���һ������
�������������У���һ������![]() �����������ı���
�����������ı���![]() ��
��![]() �������DZ�
�������DZ�![]() �ָ�ɵġ��Ѻ��ı��Ρ����� ��
�ָ�ɵġ��Ѻ��ı��Ρ����� ��
��2����ͼ2����![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת�õ�
��ʱ����ת�õ�![]() ����
����![]() ���ڱ�
���ڱ�![]() ������
������![]() ��
��![]() ��
��![]() ���ӳ����ڵ�
���ӳ����ڵ�![]() ����֤���ı���
����֤���ı���![]() �ǡ��Ѻ��ı��Ρ���
�ǡ��Ѻ��ı��Ρ���
��3����ͼ3����![]() �У�
��![]() ��
��![]() ��
��![]() �����Ϊ
�����Ϊ![]() ����
����![]() ��
��![]() ��ƽ������һ�㣬����
��ƽ������һ�㣬����![]() ��
��![]() �����ı���
�����ı���![]() �DZ�
�DZ�![]() �ָ�ɵġ��Ѻ��ı��Ρ�����
�ָ�ɵġ��Ѻ��ı��Ρ�����![]() �ij���
�ij���
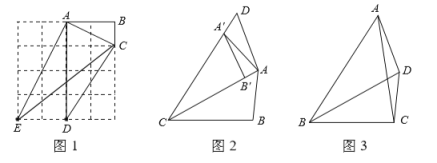
���𰸡���1���ı���![]() ����2�������������3��
����2�������������3��![]()
��������
��1���������������Ƶ��ж���������ABC~EAC���������ɵõ��𰸣�
��2������ת�����ʵã�![]() ��
��![]() �����
�����![]() ����
����![]() ���������ɵõ����ۣ�
���������ɵõ����ۣ�
��3������![]() ��
��![]() ��
��![]() ����
����![]() ����������������
����������������![]() �����
�����![]() ��
��![]() �����ɵõ��𰸣�
�����ɵõ��𰸣�
��1��������ã�![]() ,
,
��![]() ��
��
��ABC~EAC��
�౻![]() �ָ�ɵġ��Ѻ��ı��Ρ����ǣ��ı���
�ָ�ɵġ��Ѻ��ı��Ρ����ǣ��ı���![]() ��
��
�ʴ��ǣ��ı���![]() ��
��
��2��������ת�����ʵã�![]() ��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��![]() ��
��
���ı���![]() �ǡ��Ѻ��ı��Ρ���
�ǡ��Ѻ��ı��Ρ���
��3������![]() ��
��![]() ��
��![]() ��
��
����![]() ��
��![]() ��
��
��![]() �����Ϊ
�����Ϊ![]() ��
��
��![]() ��
��
��![]() ��
��
���ı���![]() �DZ�
�DZ�![]() �ָ�ɵġ��Ѻ��ı��Ρ�����
�ָ�ɵġ��Ѻ��ı��Ρ�����![]() ��
��
��![]() ��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��


 �����ҵ���������ϵ�д�
�����ҵ���������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
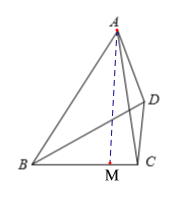
����Ŀ����ͼ����ƽ���ı���ABCD�У�AE��BD��E��
��1����BC��BD��![]() ��AD��15�����ABD���ܳ���
��AD��15�����ABD���ܳ���
��2������DBC��45�㣬�Խ���AC��BD���ڵ�O��FΪAE��һ�㣬��AF��2EO����֤��CF��![]() AB��
AB��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������MNOK����������ABCDEF�߳���Ϊ1���������η������������У�ʹOK����AB���غϣ���ͼ��ʾ�������в�����������������������������Ƶ�B˳ʱ����ת��ʹKM����BC���غϣ���ɵ�һ����ת�����Ƶ�C˳ʱ����ת��ʹMN����CD���غϣ���ɵڶ�����ת������������������ת������ת�Ĺ����У��������κ��������εı��غ�ʱ����B��M��ľ�������ǣ�������
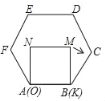
A. 0.5B. 0.7C. ![]() ��1D.
��1D. ![]() ��1
��1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
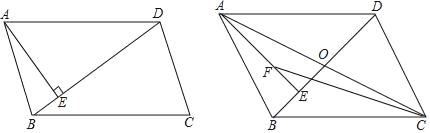
����Ŀ����ͼ��ABCD�У��Խ���AC��BD�ཻ�ڵ�O�����AC=12��BD=10��AB=m����ôm��ȡֵ��Χ�ǣ�������
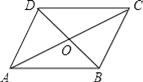
A. 1��m��11 B. 2��m��22 C. 10��m��12 D. 5��m��6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���![]() ��ͼ���뷴��������
��ͼ���뷴��������![]() ��ͼ���ཻ��
��ͼ���ཻ��![]() ��
��![]() ���㣬���е�
���㣬���е�![]() ������Ϊ
������Ϊ![]() ����
����![]() ������Ϊ
������Ϊ![]() .
.
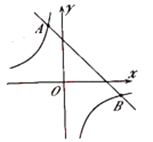
��1������ͼ��ֱ��д������![]() ��
��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2���������������ı���ʽ��
��3����![]() ���߶�
���߶�![]() �ϣ���
�ϣ���![]() �����
�����![]() ������.
������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�߶�![]() ��
�� ![]() ��
��![]() �ϵ�һ���㣬
�ϵ�һ���㣬![]() ��
��![]() ���е㣬��
���е㣬��![]() Ϊ����������
����������![]() ����
����![]() ��������
��������![]() �ĶԳƵ�Ϊ
�ĶԳƵ�Ϊ![]() ������
������![]() ��
��![]() ��ֱ��
��ֱ��![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��
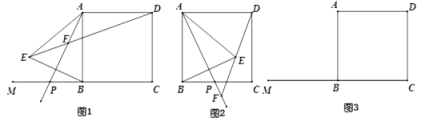
��1����ͼ1������![]() ���߶�
���߶�![]() �ϣ���
�ϣ���![]() ����
����![]() �Ķ�����
�Ķ�����
��2��С���ڽ���ʱ���֣�����![]() ���߶�
���߶�![]() ��ʱ���߶�
��ʱ���߶�![]() ��
��![]() ��
��![]() ֮������
֮������![]() ����ô����Ϊ����
����ô����Ϊ����![]() ���߶�
���߶�![]() ��ʱ����ͼ2�������Ľ����Ƿ���������������֤����������������˵�����ɣ�
��ʱ����ͼ2�������Ľ����Ƿ���������������֤����������������˵�����ɣ�
��3����ͼ3����![]() ��
��![]() �ϣ���
�ϣ���![]() ������
������![]() �ӵ�
�ӵ�![]() �˶�����
�˶�����![]() ʱ��ֱ��д����
ʱ��ֱ��д����![]() ��������·������
��������·������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��P��1��3����Q��3��m���Ǻ���![]() ͼ��������.
ͼ��������.
��1����kֵ��mֵ.
��2��ֱ��![]() ��
��![]() ��ͼ����A��ֱ��
��ͼ����A��ֱ��![]() ��ֱ��
��ֱ��![]() ƽ�У���x�ύ�ڵ�B������
ƽ�У���x�ύ�ڵ�B������![]() ��ͼ���ڵ�C.���߶�OA��OB�� BC������
��ͼ���ڵ�C.���߶�OA��OB�� BC������![]() ͼ����AC֮�䲿��Χ�ɵ������ڣ������߽磩ǡ��2�����㣬��Ϻ���ͼ��ֱ��д��b��ȡֵ��Χ.��ע�����������Ϊ�����ĵ��Ϊ���㣩
ͼ����AC֮�䲿��Χ�ɵ������ڣ������߽磩ǡ��2�����㣬��Ϻ���ͼ��ֱ��д��b��ȡֵ��Χ.��ע�����������Ϊ�����ĵ��Ϊ���㣩
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ҵǰ�갴�ɻ�������������15Ԫ/�֡����ɻ�������������25Ԫ/�ֵ��շѱ�����֧����������������5000Ԫ����ȥ��Ԫ�����շѱ��ϵ�Ϊ���ɻ�������������30Ԫ/�֣����ɻ�������������100Ԫ/�֣�������ҵȥ�괦��������������������ǰ�����û�б仯�������ۺ��Ҫ��֧��������9000Ԫ��
��1������ҵǰ�괦���Ŀɻ��������Ͳ��ɻ������������ٶ֣�
��2������ҵ�ƻ����꽫�����������������������ٵ�200�֣��ҿɻ������������ڲ��ɻ���������������3������������ҵ�����ж��ٶֿɻ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
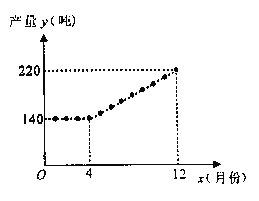
����Ŀ�������������鷢�������������г���Ӧ����ƫ�������۴������ʱ�з�����Ϊ�ȶ������������ٽ�ת����������ǿ���Ӧ��������������Ժ�칫����2019��9��ӡ���ˡ������ȶ����������ٽ�ת���������������ij����������������Ӧ���Һ��٣�Ŭ�����������Ӫ����ˮƽ���Ȳ�������ֳ��ģ���������Ӧ������������2019��ÿ����������y���֣����·�x��![]() ����xΪ������֮��ĺ�����ϵ��ͼ��ʾ.
����xΪ������֮��ĺ�����ϵ��ͼ��ʾ.
��1����ֱ��д����![]() ��xΪ��������
��xΪ��������![]() ��xΪ������ʱ��y��x�ĺ�����ϵʽ��
��xΪ������ʱ��y��x�ĺ�����ϵʽ��
��2��������������������P����Ԫ/�֣����·�x��![]() ����xΪ�����������ϵʽ��
����xΪ�����������ϵʽ��![]() �����ʣ����������ĸ��µ����������������Ƕ��٣�
�����ʣ����������ĸ��µ����������������Ƕ��٣�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com