
【题目】如图,△ABC和△ADE均为等腰直角三角形,![]() ,B、C、E三点共线,BE平分∠AED,F为CD的中点,AF、AC的延长线分别交DE于H、G点。
,B、C、E三点共线,BE平分∠AED,F为CD的中点,AF、AC的延长线分别交DE于H、G点。
求证:⑴![]() ; ⑵
; ⑵![]()

【答案】见解析
【解析】
⑴通过△ABC和△ADE均为等腰直角三角形,∠AED=∠BAC=90°,证明∠AGD=∠GAD即可;
(2)延长AF至k点,使AF=FK,连接DK,则AF=![]() AK,证明△ACF≌△KDF得DK=AC=AB,∠CAF=∠K,再证明△AEB≌△KDA即可.
AK,证明△ACF≌△KDF得DK=AC=AB,∠CAF=∠K,再证明△AEB≌△KDA即可.
⑴∵BE平分∠AED,△ADE为等腰直角三角形
∴∠AEC=∠BED=22.5°
∵∠AED=∠BAC=90°
∴∠GAE=∠BAD
∵△ABC为等腰直角三角形
∴∠BCA=45°
∴∠ECA=135°
∵∠AEC =22.5°
∴∠GAE=22.5°=∠BAD
∴∠AGD=∠AEG+∠EAG=67.5°
∠GAD=∠EAD-∠EAG=67.5°.
∴∠AGD=∠GAD.
∴AD=AG.

(2)延长AF至k点,使AF=FK,连接DK,则AF=![]() AK;
AK;
∵F为CD的中点
∴CF=FD
在△ACF和△KDF中,CF=FD,∠CFA=∠DFK,AF=FK
∴△ACF≌△KDF
∴DK=AC=AB,∠CAF=∠K
∴∠KDA+∠CAD=180°
∵∠EAB+∠CAD=180°
∴∠KDA=∠EAB
在△AEB和△KDA中, ∠KDA=∠EAB, DK=AC,AE=AD
∴△AEB≌△KDA
∴BE=AK
∴![]()


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线AB:![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() .过点
.过点![]() 作
作![]() 轴的垂线
轴的垂线![]() 交
交![]() 于点
于点![]() ,点
,点![]() 从点
从点![]() 出发,沿着射线
出发,沿着射线![]() 的方向向上运动,设
的方向向上运动,设![]() .
.
(1)直线![]() 的函数表达式;
的函数表达式;
(2)求![]() 的面积(用含
的面积(用含![]() 的代数式表示);
的代数式表示);
(3)若以![]() 为直角顶点,
为直角顶点,![]() 为直角边在第一象限作等腰直角三角形
为直角边在第一象限作等腰直角三角形![]() ,随着点
,随着点![]() 的运动,点
的运动,点![]() 是否也在同一直线上运动?若在同一直线上运动,请求出直线表达式;若不在同一直线上运动,请说明理由.
是否也在同一直线上运动?若在同一直线上运动,请求出直线表达式;若不在同一直线上运动,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
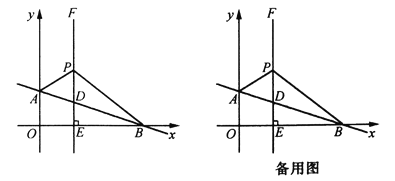
【题目】如图所示,OE,OD分别平分∠AOC和∠BOC,
(1)如果∠AOB=90°,∠BOC=38°,求∠DOE的度数;
(2)如果∠AOB=α,∠BOC=β(α、β均为锐角,α>β),其他条件不变,求∠DOE;
(3)从(1)、(2)的结果中,你发现了什么规律,请写出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
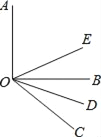
【题目】如图,直线![]() 、
、![]() 相交于点
相交于点![]() ,
,![]() 平分
平分![]() .
.
(1)若![]() ,求
,求![]() 的度数;
的度数;
(2)若![]() 平分
平分![]() ,∠BOF=12°,若设∠BOE=x°.
,∠BOF=12°,若设∠BOE=x°.
①则![]() = . (用含
= . (用含![]() 的代数式表示)
的代数式表示)
②求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】金秋十月,长沙市某中学组织七年级学生去某综合实践基地进行秋季社会实践活动,每人需购买一张门票,该综合实践基地的门票价格为每张240元,如果一次购买500张以上(不含500张)门票,则门票价格为每张220元,请回答下列问题:
(1)列式表示n个人参加秋季社会实践活动所需钱数;
(2)某校用132000元可以购买多少张门票;
(3)如果我校490人参加秋季社会实践,怎样购买门票花钱最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017通辽)小兰和小颖用下面两个可以自由转动的转盘做游戏,每个转盘被分成面积相等的几个扇形,转动两个转盘各一次,若两次指针所指数字之和小于4,则小兰胜,否则小颖胜(指针指在分界线时重转),这个游戏对双方公平吗?请用树状图或列表法说明理由. 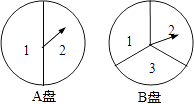
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(-5a4)·(-8ab2)=_______;
(2)(-![]() x2yz2)2·(3xy2)2=_______;
x2yz2)2·(3xy2)2=_______;
(3)a(2-a)-2(a+1)=________;
(4)(4x2-3x+6)·(-![]() x)=_______;
x)=_______;
(5)3x2y·(![]() x3y2)·(5xy2)=________
x3y2)·(5xy2)=________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面内的两条直线有相交和平行两种位置关系.
(1)如图1,若AB∥CD,点P在AB、CD内部,∠B=50°,∠D=30°,求∠BPD.
(2)如图2,将点P移到AB、CD外部,则∠BPD、∠B、∠D之间有何数量关系?(不需证明)
(3)如图3,写出∠BPD﹑∠B﹑∠D﹑∠BQD之间的数量关系?请证明你的结论.
(4)如图4,求出∠A+∠B+∠C+∠D+∠E+∠F的度数.


查看答案和解析>>
科目:初中数学 来源: 题型:
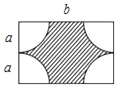
【题目】如图所示的是某居民小区的一块长为bm,宽为2am的长方形空地,为了美化环境,准备在这个长方形空地的四个顶点各修建一个半径为am的扇形花台,然后在花台内种花,其余空地种草,如果建筑花台及种花每平方米需要资金200元,种草每平方米需要资金150元,那么美化这块空地共需资金多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com