
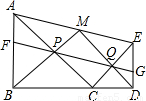
 BD,则∠BMD=90°,判断①正确;
BD,则∠BMD=90°,判断①正确; AE,又AF∥EG,根据两组对边分别平行的四边形是平行四边形可判断②正确;
AE,又AF∥EG,根据两组对边分别平行的四边形是平行四边形可判断②正确; AE,则FP+GQ=
AE,则FP+GQ= AE=PQ,判断③正确;
AE=PQ,判断③正确;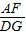 =
= ,同理△BPF∽△EQG,
,同理△BPF∽△EQG,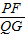 =
=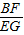 ,则
,则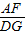 =
= ,AF•EG=BF•DG,又AF=EG,判断④正确.
,AF•EG=BF•DG,又AF=EG,判断④正确.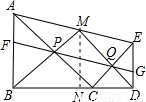 解:①过点M作MN⊥BD,垂足为N,则MN∥DE∥AB,
解:①过点M作MN⊥BD,垂足为N,则MN∥DE∥AB, (AB+ED)=
(AB+ED)= (BC+CD)=
(BC+CD)= BD=BN=ND,
BD=BN=ND, AE,
AE, AE,
AE, AE=
AE= AE=PQ,
AE=PQ,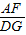 =
=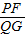 ,
,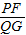 =
= ,
, =
=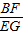 ,
,

科目:初中数学 来源: 题型:

| BG | CG |
查看答案和解析>>
科目:初中数学 来源: 题型:
 10、如图,△ABC和△ADE都是等腰直角三角形,∠ACB和∠AED都是直角,点C在AD上,如果△ABC经旋转后能与△ADE重合,那么点
10、如图,△ABC和△ADE都是等腰直角三角形,∠ACB和∠AED都是直角,点C在AD上,如果△ABC经旋转后能与△ADE重合,那么点查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,△ABC和△CDE均为等腰直角三角形,点B,C,D在一条直线上,点M是AE的中点,BC=3,CD=1.
如图,△ABC和△CDE均为等腰直角三角形,点B,C,D在一条直线上,点M是AE的中点,BC=3,CD=1.| BC | CD |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,四边形ACDE是平行四边形,连接CE交AD于点F,连接BD交 CE于点G,连接BE.下列结论中:
如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,四边形ACDE是平行四边形,连接CE交AD于点F,连接BD交 CE于点G,连接BE.下列结论中:查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,△ABC和△ADE都是等腰直角三角形,AB=AC,AD=AE,∠BAC=∠DAE=90°.
如图,△ABC和△ADE都是等腰直角三角形,AB=AC,AD=AE,∠BAC=∠DAE=90°.| 2 |
| 10 |
| 10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com